Research Article
Meromorphic or Holomorphic Completion of a Reinhardt Domain
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-12
-
- Article
-
- You have access
- Export citation
Note on the Infinite Dimensional Laplacian Operator
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 13-19
-
- Article
-
- You have access
- Export citation
On a Class of Metrical Automorphisms on Gaussian Measure Space
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 21-25
-
- Article
-
- You have access
- Export citation
A Characterization of the Simple Group U3(5)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 27-40
-
- Article
-
- You have access
- Export citation
Stochastic Integrals Based on Martingales Taking Values in Hilbert Space
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 41-52
-
- Article
-
- You have access
- Export citation
On a Homology Theory Associated to Foliations
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 53-61
-
- Article
-
- You have access
- Export citation
Some Remarks on Evaluations of the Primitive Logic
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 63-69
-
- Article
-
- You have access
- Export citation
Sur Le Schéma de la Séparation*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 71-84
-
- Article
-
- You have access
- Export citation
On Principal Function Problem
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 85-90
-
- Article
-
- You have access
- Export citation
A Remark on the Moyal’s Construction of Markov Processes
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 91-101
-
- Article
-
- You have access
- Export citation
On a Necessary Condition for the Sample Path Continuity of Weakly Stationary Processes
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 103-111
-
- Article
-
- You have access
- Export citation
A Determinate Logic
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 113-138
-
- Article
-
- You have access
- Export citation
On a Π01 Set of Positive Measure
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 139-144
-
- Article
-
- You have access
- Export citation
On a Propositional Calculus Whose Decision Problem is Recursively Unsolvable1)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-152
-
- Article
-
- You have access
- Export citation
Prolongations of G-Structures to Tangent Bundles of Higher Order
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 153-179
-
- Article
-
- You have access
- Export citation
The Topological Support of Gauss Measure on Hilbert Space
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 181-183
-
- Article
-
- You have access
- Export citation
Introduction of a Basic Theory of Objects
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 185-225
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 38 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 38 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation



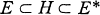
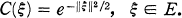
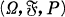 be a probability space and suppose we are given a family of σ-fields
be a probability space and suppose we are given a family of σ-fields 
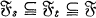 for O ≤
for O ≤ 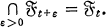 .
. in
in  in
in 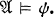
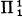 sets which have positive measure (or which are not meager, i.e., of the second Baire category) have been obtained by several authors. For example, every non-meager
sets which have positive measure (or which are not meager, i.e., of the second Baire category) have been obtained by several authors. For example, every non-meager 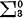 set must have a recursive element (Shoenfield-Hinman, Hinman [2]) but there exists a non-meager
set must have a recursive element (Shoenfield-Hinman, Hinman [2]) but there exists a non-meager 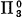 set (as well as of measure 1) that contains no recursive element (Shoenfield [7]), and every
set (as well as of measure 1) that contains no recursive element (Shoenfield [7]), and every 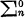 set (i.e., arithmetic set) of positive measure contains an arithmetic element (Sacks [5], and Tanaka [12]).
set (i.e., arithmetic set) of positive measure contains an arithmetic element (Sacks [5], and Tanaka [12]).