Research Article
Voronoĭ's conjecture and space tiling zonotopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-10
-
- Article
- Export citation
Stochastical approximation of smooth convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 11-29
-
- Article
- Export citation
Random polytopes in smooth convex bodies: corrigendum
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 31
-
- Article
- Export citation
The Santaló point of a function, and a functional form of the Santaló inequality
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 33-48
-
- Article
- Export citation
A generalization of some lattices of Coxeter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 49-61
-
- Article
- Export citation
On a problem of Granville and Zhu Regarding Pascal's triangle
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-82
-
- Article
- Export citation
The values of ternary quadratic forms at prime arguments
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-96
-
- Article
- Export citation
An improvement of Artin's conjecture on average for composite moduli
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-109
-
- Article
- Export citation
Completely 0-simple semigroups of left quotients
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-122
-
- Article
- Export citation
On the non-homogeneous quadratic Bessel zeta function
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 123-130
-
- Article
- Export citation
The values of Mahler measures
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-148
-
- Article
- Export citation
A characterization of the barycentre
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-153
-
- Article
- Export citation
Families of surfaces lying in a null set
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-162
-
- Article
- Export citation
Fell continuous selections and topologically well-orderable spaces
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 163-169
-
- Article
- Export citation
Trapped modes in a waveguide with a thick obstacle
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-186
-
- Article
- Export citation
Positive solutions for Dirichlet problems of singular quasilinear elliptic equations via variational methods
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 187-202
-
- Article
- Export citation
Book Reviews
Book Reviews - S. Alaca and K. S. Williams. Introductory Algebraic Number Theory. Cambridge University Press, 2004; 428 pp. ISBN 0 521 83250 0 (hardback), £65; 0 521 54011 9 (paperback), £24.99. - A. Baker and B. Richter (editors). Structured Ring Spectra. London Mathematical Society Lecture Note Series 315, Cambridge University Press. 2004; 236 pp. ISBN 0 521 60305 6 (paperback), £35. - R. Beals. Analysis: an Introduction. Cambridge University Press, 2004; 261 pp. ISBN 0 521 84072 4 (hardback), £50; 0 521 60047 2 (paperback), £24.99. - B. Bollobás. Random Graphs (2nd edition). Cambridge University Press, 2001; 498 pp. ISBN 0 521 80920 7 (hardback), £75; 0 521 79722 5 (paperback), £29.95. - J. A. Buchmann. Introduction to Cryptography (2nd edition). Undergraduate Texts in Mathematics, Springer-Verlag (Berlin-Heidelberg), 2004; 335 pp. ISBN 0 387 21156 X (hardback), £61.50; 0 387 20756 2 (paperback). £30.50. - Y. Bugeaud. Approximation by Algebraic Numbers. Cambridge Tracts in Mathematics 160, Cambridge University Press, 2004; 274 pp. ISBN 0 521 82329 3 (hardback), £40. - D. Cvetković, P. Rowlinson and S. Simić. Spectral Generalizations of Line Graphs: On Graphs with Least Eigenvalue 2. London Mathematical Society Lecture Note Series 314, Cambridge University Press. 2004; 298 pp. ISBN 0 521 83663 8 (paperback), £35. - H. Darmon and S.-W. Zhang (editors). Heegner Points and Rankin L-Series. MSRI Publications 49, Cambridge University Press, 2004; 367 pp. ISBN 0 521 83659 X (hardback), £45. - A. K. Dewdney. Beyond Reason: Eight Great Problems that Reveal the Limits of Science. John Wiley and Sons Inc. (Hoboken, NJ), 2004; 224 pp. ISBN 0 471 01398 6 (hardback), £19.99. - G. Gasper and M. Rahman. Basic Hypergeometric Series {2nd edition). Encyclopedia of Mathematics and its Applications 96, Cambridge University Press, 2004; 428 pp. ISBN 0 521 83357 4 (hardback), £65. - M. Georgiadou. Constantin Caratheodory: Mathematics and Politics in Turbulent Times. Springer-Verlag (Berlin), 2004; 651 pp. ISBN 3 540 20352 4 (paperback), £30.50. - C. G. Gibson. Elementary Euclidean Geometry: An Undergraduate Introduction. Cambridge University Press, 2003; 174 pp. ISBN 0 521 83448 1 (hardback), £32.50. - M. C. Golumbic and A. N. Trenk. Tolerance Graphs. Cambridge Studies in Advanced Mathematics 89, Cambridge Universtiy Press, 2004; 265 pp. ISBN 0 521 82758 2 (hardback), £40. - L. H. Harper. Global Methods for Combinatorial Isoperimetric Problems. Cambridge Studies in Advanced Mathematics 90, Cambridge University Press, 2004; 232 pp. ISBN 0 521 83268 3 (hardback), £40. - H. Kurzweil and B. Stellmacher. The Theory of Finite Groups: An Introduction. Springer Universitext, Springer-Verlag (New York-Berlin-Heidelberg), 2004; 387 pp. ISBN 0 387 40510 0 (hardback), £54. - J. H. Kwak and S. Hong. Linear Algebra (2nd edition). Birkhäuser (Boston), 2004; 390 pp. ISBN 0 8176 4294 3 (paperback), £39 (approx.) - T. Y. Lam. Exercises in Classical Ring Theory (2nd edition). Problem Books in Mathematics, Springer-Verlag (New York-Berlin-Heidelberg), 2003: 359 pp. ISBN 0 387 00500 5 (hardback), £54. - K. Mccrlmmon. A Taste of Jordan Algebras. Springer Universitext. Springer-Verlag (New York-Berlin-Heidelberg), 2004; 562 pp. ISBN 0 387 95447 3 (hardback), £57.50. - A. A. Mikhalev, V. Shpilrain and J.-T. Yu. Combinational Methods, Free Groups, Polynomials and Free Algebras. Canadian Mathematical Society Books in Mathematics 19, Springer, 2004; 315 pp. ISBN 0 387 40562 3 (hardback), £69. - M. C. Pedicchio and W. Tholen. Categorical Foundations: Special Topics in Order, Topology, Algebra and Sheaf Theory. Encyclopedia of Mathematics and its Applications 97, Cambridge University Press, 2004; 417 pp. ISBN 0 521 83414 7 (hardback), £60. - M. Reid and A. Skorobogatov. Number Theory and Algebraic Geometry. London Mathematical Society Lecture Note Series 303, Cambridge University Press, 2003; 300 pp. ISBN 0 521 54518 8 (paperback), £35. - H. K. Schenck. Computational Algebraic Geometry. London Mathematical Society Student Texts 58, Cambridge University Press, 2003; 193 pp. ISBN 0 521 82964 X (hardback), £50; 0 521 53650 2 (paperback), £18.99. - J. Stedall (translator). The Arithmetic of Infinitesimals: John Wallis 1656. Sources and Studies in the History of Mathematics and Physical Sciences, Springer (New York), 2004; 192 pp. ISBN 0 387 20709 0 (hardback), £92.50. - C. Teuscher (editor). Alan Turing: Life and Legacy of a Great Thinker. Springer-Verlag (Berlin-Heidelberg-New York), 2004; 542 pp. ISBN 3 540 20020 7 (hardback), £46. - C. T. C. Wall. Singular Points of Plane Curves. London Mathematical Society Student Texts 63, Cambridge University Press, 2004; 370 pp. ISBN 0 521 83904 1 (hardback), £55; 0 521 54774 1 (paperback), £27. - A. H. Zemanian. Graphs and Networks, Transfinite and Non-standard. Birkhäuser (Boston), 2004; 202 pp. ISBN 0 8176 4292 7 (paperback). £65 (approx.).
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 203-208
-
- Article
- Export citation
Index
Index to volume 51
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 209
-
- Article
- Export citation
Front matter
MTK volume 51 issue 1-2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
-
- Article
-
- You have access
- Export citation

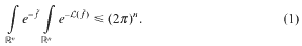
 ends with
ends with 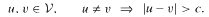
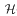 -class of
-class of 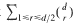 with all its roots lying in the Galois closure
with all its roots lying in the Galois closure 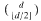 over ℚ This is used to show that some numbers considered earlier by Boyd are not Mahler measures. The set of numbers which occur as Mahler measures of both reciprocal and nonreciprocal algebraic numbers is also investigated. In particular, all cubic units in this set are described and it is shown that the smallest Pisot number is not the measure of a reciprocal number.
over ℚ This is used to show that some numbers considered earlier by Boyd are not Mahler measures. The set of numbers which occur as Mahler measures of both reciprocal and nonreciprocal algebraic numbers is also investigated. In particular, all cubic units in this set are described and it is shown that the smallest Pisot number is not the measure of a reciprocal number.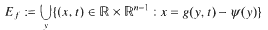
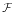 (
(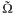 (the
(the 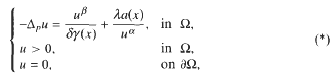
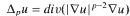 , 1 <
, 1 <