Article contents
UPPER BOUND THEOREM FOR ODD-DIMENSIONAL FLAG TRIANGULATIONS OF MANIFOLDS
Published online by Cambridge University Press: 01 June 2016
Abstract
We prove that among all flag triangulations of manifolds of odd dimension 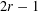 $2r-1$, with a sufficient number of vertices, the unique maximizer of the entries of the
$2r-1$, with a sufficient number of vertices, the unique maximizer of the entries of the 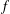 $f$-,
$f$-, 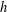 $h$-,
$h$-, 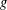 $g$- and
$g$- and 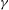 $\unicode[STIX]{x1D6FE}$-vector is the balanced join of
$\unicode[STIX]{x1D6FE}$-vector is the balanced join of  $r$ cycles. Our proof uses methods from extremal graph theory.
$r$ cycles. Our proof uses methods from extremal graph theory.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 5
- Cited by




