Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-19T04:46:25.970Z Has data issue: false hasContentIssue false
  • English
  • Français

SHORTEST DISTANCE IN MODULAR HYPERBOLA AND LEAST QUADRATIC NON-RESIDUE

Part of: Elementary number theory Exponential sums and character sums

Published online by Cambridge University Press:  10 May 2016

Tsz Ho Chan
Tsz Ho Chan*
Affiliation:
Department of Mathematical Sciences, University of Memphis, Memphis, TN 38152, U.S.A. email thchan6174@gmail.com
Get access

Abstract

In this paper, we study how small a box contains at least two points from a modular hyperbola 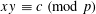$xy\equiv c\;(\text{mod}\;p)$. There are two such points in a square of side length 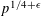$p^{1/4+\unicode[STIX]{x1D716}}$. Furthermore, it turns out that either there are two such points in a square of side length 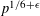$p^{1/6+\unicode[STIX]{x1D716}}$ or the least quadratic non-residue is less than 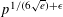$p^{1/(6\sqrt{e})+\unicode[STIX]{x1D716}}$.

MSC classification

Primary: 11A07: Congruences; primitive roots; residue systems 11A15: Power residues, reciprocity 11L40: Estimates on character sums
Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 860 - 865
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Burgess, D. A., The distribution of quadratic residues and non-residues. Mathematika 4 1957, 106–112.Google Scholar
Heath-Brown, D. R., Burgess’s bounds for character sums. In Number Theory and Related Fields (Springer Proceedings in Mathematics and Statistics 43), Springer (New York, 2013), 199–213.Google Scholar
Shao, X., Character sums over unions of intervals. Forum Math. 27(5) 2015, 3017–3026.Google Scholar
Shparlinski, I., Modular hyperbolas. Jpn. J. Math. 7(2) 2012, 235–294.Google Scholar
Shparlinski, I., Multiple exponential and character sums with monomials. Mathematika 60(2) 2014, 363–373.Google Scholar
Vinogradov, I. M., On a general theorem concerning the distribution of the residues and non-residues of powers. Trans. Amer. Math. Soc. 29 1927, 209–217.CrossRefGoogle Scholar