Research Article
On certain soluble groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-4
-
- Article
- Export citation
Subalgebras of modular annihilator algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-12
-
- Article
- Export citation
A counter-example to the three balls problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 13-16
-
- Article
- Export citation
On transversality
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 17-20
-
- Article
- Export citation
Isotopy classes of embeddings and homotopy
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 21-26
-
- Article
- Export citation
A note on nth roots of positive operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 27-30
-
- Article
- Export citation
Lipschitz classes on finite dimensional groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-38
-
- Article
- Export citation
On ‘translated quasi-Cesàro’ summability. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 39-41
-
- Article
- Export citation
Sums of three roots of unity. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-59
-
- Article
- Export citation
On rational primes p congruent to 1 (mod 3 or 5)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 61-70
-
- Article
- Export citation
Two singular integral equations involving confluent hypergeometric functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 71-89
-
- Article
- Export citation
Expansions for Kν(ξ) involving Airy's function†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 91-94
-
- Article
- Export citation
Some results on generalized hypergeometric polynomials†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 95-104
-
- Article
- Export citation
Bilateral generating functions involving Jacobi polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 105-107
-
- Article
- Export citation
A note on the summation of divergent power series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-114
-
- Article
- Export citation
Quadratic Lyapunov functions for linear systems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 115-117
-
- Article
- Export citation
Exact solutions for fields of electric type in spherically stratified isotropic media
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-127
-
- Article
- Export citation
Exact solutions for transverse electromagnetic wave propagation in a cylindrically stratified axially magnetized plasma
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-143
-
- Article
- Export citation
A new interpretation of the NUT metric in general relativity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-151
-
- Article
- Export citation
Impossibility of class one electromagnetic fields
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 153-154
-
- Article
- Export citation



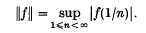
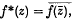 and also ‖
and also ‖
 , and
, and 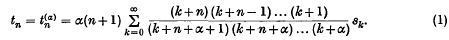

 the maximum absolute value of α and all its algebraic conjugates. We say that α and β are
the maximum absolute value of α and all its algebraic conjugates. We say that α and β are 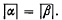
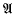 ,
, 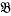 ,
, 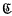 , or
, or 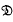 ,
, 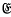 respectively, by letting
respectively, by letting 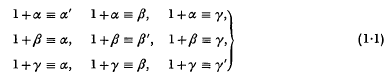
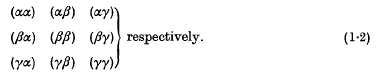
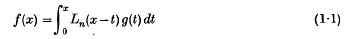
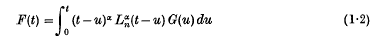
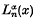 and Whittaker functions
and Whittaker functions 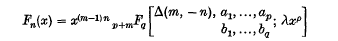
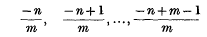
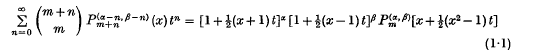
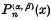 is denned as ((3), p. 255)
is denned as ((3), p. 255)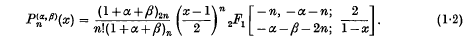
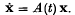 The derivative
The derivative