Research Article
Cushions, cigars and diamonds: an area-perimeter problem for symmetric ovals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-16
-
- Article
- Export citation
On triangle contractive operators in Hilbert spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 17-20
-
- Article
- Export citation
The modular curve X0(39) and rational isogeny
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 21-23
-
- Article
- Export citation
The arithmetic plurigenera of surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-31
-
- Article
- Export citation
Intersection multiplicities and tangent cones
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-42
-
- Article
- Export citation
An application of p-factorization methods to symmetric graphs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-48
-
- Article
- Export citation
Representations and automorphisms of some wreath products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-53
-
- Article
- Export citation
A theorem on integral closures of ideals in semi-local rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 55-59
-
- Article
- Export citation
Consistency conditions for a finite set of projections of a function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 61-68
-
- Article
- Export citation
On harmonic functions which take integer values on integer lattices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 69-77
-
- Article
- Export citation
On dichotomy of Riesz products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-89
-
- Article
- Export citation
Homotopy colimits in the category of small categories
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 91-109
-
- Article
- Export citation
A remark on the construction of random measures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-115
-
- Article
- Export citation
Unconditional bases and martingales in LP(F)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-123
-
- Article
- Export citation
Generic bifurcations of forced oscillations of integrable mechanical systems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 125-142
-
- Article
- Export citation
Euler operators and conservation laws of the BBM equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 143-160
-
- Article
- Export citation
Singularities, incompleteness and the Lorentzian distance function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-178
-
- Article
- Export citation
Theoretical plasticity of textured aggregates
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-191
-
- Article
- Export citation
Front matter
PSP volume 85 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 85 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation



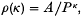
 , where there is no given upper bound on
, where there is no given upper bound on  , when one is given a bound
, when one is given a bound 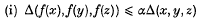
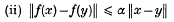
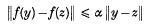
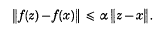
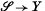 say, with fibre ρ
say, with fibre ρ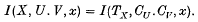
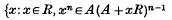 of
of 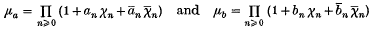
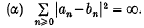
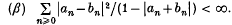
 with
with