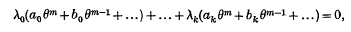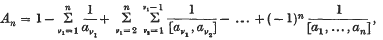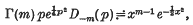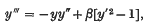Research Article
The envelope of the subspaces of the polyhedra of an involution on a rational curve
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-187
-
- Article
- Export citation
Projective characters and invariants of algebraic varieties
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 188-198
-
- Article
- Export citation
On certain surfaces which have unpostulated singularities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-206
-
- Article
- Export citation
On an inequality in the elementary theory of numbers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 207-209
-
- Article
- Export citation
An infinite integral involving Bessel functions and parabolic cylinder functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 210-211
-
- Article
- Export citation
The “closest” estimates of statistical parameters
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 212-222
-
- Article
- Export citation
On an equation occurring in Falkner and Skan's approximate treatment of the equations of the boundary layer
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 223-239
-
- Article
- Export citation
The effect of configuration interaction on the low terms of the spectra of oxygen
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 240-249
-
- Article
- Export citation
A note on molecular orbitals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 250-252
-
- Article
- Export citation
A comparison of wave functions for the normal helium atom
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 253-259
-
- Article
- Export citation
Superconducting cylinders
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 260-276
-
- Article
- Export citation
The generalized Fermi interaction
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-292
-
- Article
- Export citation
Front matter
PSP volume 33 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 33 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
-
- Article
-
- You have access
- Export citation