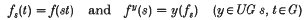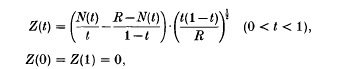Research Article
A diophantine problem in harmonic analysis
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 417-420
-
- Article
- Export citation
Uniform upper bounds for the complex divisor function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-427
-
- Article
- Export citation
On the Jacobson radical of semigroup rings of commutative semigroups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 429-433
-
- Article
- Export citation
Entropy, character theory and centrality of finite quasigroups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 435-443
-
- Article
- Export citation
On (q + t)-arcs of type (0, 2, t) in a desarguesian plane of order q
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 445-459
-
- Article
- Export citation
On the geometry of harmonic morphisms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 461-466
-
- Article
- Export citation
One-relator surface groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 467-474
-
- Article
- Export citation
Homotopy skein modules of orientable 3-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 475-488
-
- Article
- Export citation
A calculus for rational tangles: applications to DNA recombination
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 489-515
-
- Article
- Export citation
Characteristic classes of Galois representations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 517-522
-
- Article
- Export citation
Copies of l∞ in an operator space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 523-526
-
- Article
- Export citation
The uniform compactification of a locally compact abelian group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 527-538
-
- Article
- Export citation
Toeplitz operators associated with analytic crossed products
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 539-549
-
- Article
- Export citation
Entire functions with Julia sets of zero measure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 551-557
-
- Article
- Export citation
Some recent developments concerning asymptotic distributions of pontograms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 559-567
-
- Article
- Export citation
The flow near non-trivial minimal sets on 2-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 569-573
-
- Article
- Export citation
Bifurcation of periodic solutions near a collision of eigenvalues of opposite signature
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 575-601
-
- Article
- Export citation
Proceedings at the meetings
Proceedings of the meetings held during the session 1989–1990
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 603-608
-
- Article
- Export citation
Front matter
PSP volume 108 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 108 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b5
-
- Article
-
- You have access
- Export citation




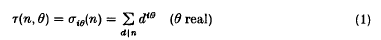
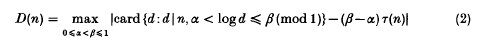
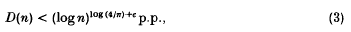


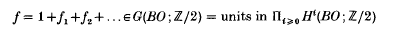
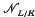 denote the multiplicative transfer (see e.g. [3,
denote the multiplicative transfer (see e.g. [3,