Research Article
In memory of the Rev. William Cecil, M.A., sometime Fellow of Magdalene College and Fellow of the Cambridge Philosophical Society
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-14
-
- Article
- Export citation
Preliminary Note on the Masses of the Electron, the Proton, and the Universe
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 15-19
-
- Article
- Export citation
On elliptic quartic curves with assigned points and chords
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 20-23
-
- Article
- Export citation
Note on some linear Diophantine inequalities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 24-25
-
- Article
- Export citation
Corrigenda
Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 25
-
- Article
-
- You have access
- Export citation
Research Article
On the Operational Solution of Linear Finite Difference Equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-36
-
- Article
- Export citation
On the Orthogonal Groups in Four Dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-48
-
- Article
- Export citation
Note on Continuous Functionals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-56
-
- Article
- Export citation
The packing of certain sets of cubes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-65
-
- Article
- Export citation
The calculation of the van der Waal forces for hydrogen and helium at large inter-atomic distances
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 66-72
-
- Article
- Export citation
Note on the Angular Scattering of Electrons in Gases
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 73-76
-
- Article
- Export citation
The Theory of the Scattering of Short X-rays by Molecular Hydrogen
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 77-85
-
- Article
- Export citation
The Diamagnetism of the Free Electron
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 86-90
-
- Article
- Export citation
On the Rotation of Dielectrics in Electrostatic Fields and Related Phenomena
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 91-102
-
- Article
- Export citation
The Photoelectric Absorption of Gamma Rays
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-112
-
- Article
- Export citation
Note on the use of a thyratron with a Geiger counter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-115
-
- Article
- Export citation
The Capture of Electrons by α-Particles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 116-130
-
- Article
- Export citation
A Mathematical Theory of Natural and Artificial Selection. Part VII. Selection intensity as a function of mortality rate
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-136
-
- Article
- Export citation
A Mathematical Theory of Natural Selection. Part VIII. Metastable Populations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 137-142
-
- Article
- Export citation
The Propagation of Electromagnetic Waves in a Refracting Medium in a Magnetic Field
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 143-162
-
- Article
- Export citation



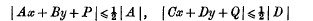
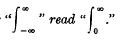
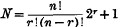 cubes. This paper discusses the possibility of completely filling space by means of the packing together of such sets of cubes.
cubes. This paper discusses the possibility of completely filling space by means of the packing together of such sets of cubes.