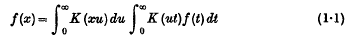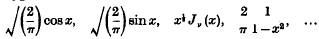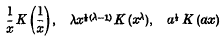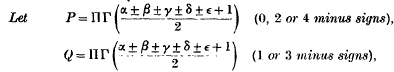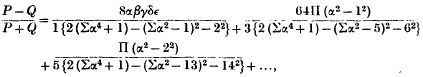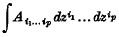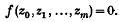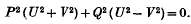Research Article
The Resultant of Two Fourier Kernels
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-6
-
- Article
- Export citation
Ramanujan's Continued Fraction
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 7-17
-
- Article
- Export citation
Some Theorems on Abelian Integrals Associated with an Algebraic Variety
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 18-25
-
- Article
- Export citation
Some Generalizations of Montel's Theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-30
-
- Article
- Export citation
On the Resolution of Cremona Transformations and particularly those of Genus One in Space of Three Dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-47
-
- Article
- Export citation
On a Class of Irregular Surfaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 48-49
-
- Article
- Export citation
The Two-Dimensional Electrostatic Solutions of Born's new Field Equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 50-68
-
- Article
- Export citation
On Subdivisions of Complexes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 69-75
-
- Article
- Export citation
On the Theory of Linear Integral Equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 76-84
-
- Article
- Export citation
Phenomena Attending the Splashing of Water in an Electric Field
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 85-93
-
- Article
- Export citation
The Electric Moment of an Electron
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 94-98
-
- Article
- Export citation
An Attempt to Detect the Neutrino
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-107
-
- Article
- Export citation
Ionization Power of a Neutrino with Magnetic Moment
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 108-115
-
- Article
- Export citation
Note on a Paper of Bell and Wolfenden on Electrolytic Separation of Diplogen
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 116-118
-
- Article
- Export citation
An Investigation of the Upper Limit of the Thorium C + C″ β-ray Spectrum by means of the Wilson Cloud Chamber
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-124
-
- Article
- Export citation
Further Investigations of the Amplitude Variations of Downcoming Wireless Waves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 125-144
-
- Article
- Export citation
Some Experiments on the Slowing Down of Neutrons by Collisions with Hydrogen Nuclei
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-152
-
- Article
- Export citation
Front matter
PSP volume 31 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 31 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation