The following note was suggested by an interesting paper written by F. P. White, where many references are given. It refers to a theorem given by W. F. Meyer, by whom the proof is indicated as possible by generalization of an intricate analytical proof given by him for a simple case. His result is that if on the rational curve of order r, in space [r], say the curve cr [r], there be an involution ∞k, of sets of m points, expressed, suppose, by an equation

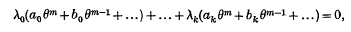
then the spaces [r − 1], formed from r points of any one of the polyhedra of m points, are an aggregate ∞k of primes of this space [r], which is of class (m − k, m − r), the notation (p, q) meaning the binomial coefficient p! / q!(p − q)!. By Meyer, the conditions k < r ≤ m are supposed to be satisfied. But there is a theorem for r < k ≤ m − 1, relating to selected [r − 1], formed from r points of any one of the polyhedra of m points. The general theorem may be formulated thus: In a space [r], the equation of any prime may be expressed by λu + μv +... + ρw = 0, where u = 0, v = 0, …w = 0 are any r + 1 given independent primes, and λ, μ, …ρ are coefficients which may be described as prime coordinates of the [r].