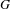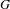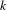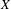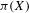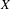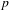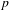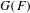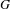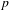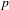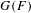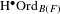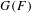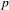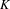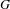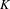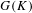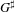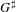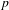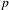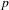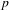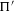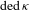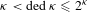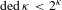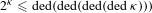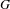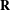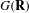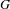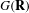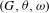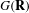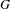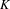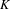Research Article
LOCAL INTERDEFINABILITY OF WEIERSTRASS ELLIPTIC FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 24 November 2014, pp. 673-691
-
- Article
- Export citation
COSIMPLICIAL SPACES AND COCYCLES
- Part of:
-
- Published online by Cambridge University Press:
- 10 November 2014, pp. 445-470
-
- Article
- Export citation
EXTENSIONS ENTRE SÉRIES PRINCIPALES
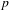 $p$-ADIQUES ET MODULO
$p$-ADIQUES ET MODULO 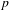 $p$ DE
$p$ DE 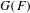 $G(F)$
$G(F)$
- Part of:
-
- Published online by Cambridge University Press:
- 08 August 2014, pp. 225-270
-
- Article
- Export citation
RIGIDITY OF CONTINUOUS QUOTIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2014, pp. 1-28
-
- Article
- Export citation
SEMIABELIAN VARIETIES OVER SEPARABLY CLOSED FIELDS, MAXIMAL DIVISIBLE SUBGROUPS, AND EXACT SEQUENCES
-
- Published online by Cambridge University Press:
- 17 July 2014, pp. 29-69
-
- Article
-
- You have access
- Export citation
THE DISTRIBUTION OF TORSION SUBSCHEMES OF ABELIAN VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2014, pp. 693-710
-
- Article
- Export citation
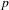 $p$-ADIC EISENSTEIN SERIES AND
$p$-ADIC EISENSTEIN SERIES AND  $L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
$L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 21 November 2014, pp. 471-510
-
- Article
- Export citation
THE RANGE OF TREE-INDEXED RANDOM WALK
- Part of:
-
- Published online by Cambridge University Press:
- 10 September 2014, pp. 271-317
-
- Article
- Export citation
ÉTALE MOTIVIC COHOMOLOGY AND ALGEBRAIC CYCLES
- Part of:
-
- Published online by Cambridge University Press:
- 24 November 2014, pp. 511-537
-
- Article
- Export citation
PROPAGATION OF SEMICLASSICAL WAVE PACKETS THROUGH AVOIDED EIGENVALUE CROSSINGS IN NONLINEAR SCHRÖDINGER EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 20 October 2014, pp. 319-365
-
- Article
- Export citation
COMPARING
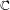 $\mathbb{C}$ AND ZILBER’S EXPONENTIAL FIELDS: ZERO SETS OF EXPONENTIAL POLYNOMIALS
$\mathbb{C}$ AND ZILBER’S EXPONENTIAL FIELDS: ZERO SETS OF EXPONENTIAL POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 04 August 2014, pp. 71-84
-
- Article
- Export citation
WHITTAKER PERIODS, MOTIVIC PERIODS, AND SPECIAL VALUES OF TENSOR PRODUCT
 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2015, pp. 711-769
-
- Article
-
- You have access
- Export citation
NONCOMMUTATIVE REAL ALGEBRAIC GEOMETRY OF KAZHDAN’S PROPERTY (T)
- Part of:
-
- Published online by Cambridge University Press:
- 30 July 2014, pp. 85-90
-
- Article
- Export citation
DERIVED LOGARITHMIC GEOMETRY I
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2014, pp. 367-405
-
- Article
- Export citation
PRO CDH-DESCENT FOR CYCLIC HOMOLOGY AND
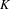 $K$-THEORY
$K$-THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 27 November 2014, pp. 539-567
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF DEDEKIND CUTS AND TWO-CARDINAL MODELS OF DEPENDENT THEORIES
-
- Published online by Cambridge University Press:
- 23 January 2015, pp. 771-784
-
- Article
- Export citation
TEMPERED SPECTRAL TRANSFER IN THE TWISTED ENDOSCOPY OF REAL GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2014, pp. 569-612
-
- Article
- Export citation
CENTER MANIFOLDS FOR PARTIALLY HYPERBOLIC SETS WITHOUT STRONG UNSTABLE CONNECTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 11 March 2015, pp. 785-828
-
- Article
-
- You have access
- Export citation
DERIVED ALGEBRAIC COBORDISM
- Part of:
-
- Published online by Cambridge University Press:
- 30 October 2014, pp. 407-443
-
- Article
- Export citation
SUR LE COMPTAGE DES FIBRÉS DE HITCHIN NILPOTENTS
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2014, pp. 91-164
-
- Article
-
- You have access
- Export citation