Article contents
CATEGORICAL PROOF OF HOLOMORPHIC ATIYAH–BOTT FORMULA
Published online by Cambridge University Press: 20 December 2018
Abstract
Given a  $2$-commutative diagram
$2$-commutative diagram
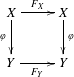
in a symmetric monoidal 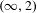 $(\infty ,2)$-category
$(\infty ,2)$-category 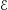 $\mathscr{E}$ where
$\mathscr{E}$ where 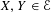 $X,Y\in \mathscr{E}$ are dualizable objects and
$X,Y\in \mathscr{E}$ are dualizable objects and  $\unicode[STIX]{x1D711}$ admits a right adjoint we construct a natural morphism
$\unicode[STIX]{x1D711}$ admits a right adjoint we construct a natural morphism  $\mathsf{Tr}_{\mathscr{E}}(F_{X})\xrightarrow[{}]{~~~~~}\mathsf{Tr}_{\mathscr{E}}(F_{Y})$ between the traces of
$\mathsf{Tr}_{\mathscr{E}}(F_{X})\xrightarrow[{}]{~~~~~}\mathsf{Tr}_{\mathscr{E}}(F_{Y})$ between the traces of 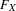 $F_{X}$ and
$F_{X}$ and 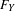 $F_{Y}$, respectively. We then apply this formalism to the case when
$F_{Y}$, respectively. We then apply this formalism to the case when 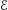 $\mathscr{E}$ is the
$\mathscr{E}$ is the 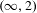 $(\infty ,2)$-category of
$(\infty ,2)$-category of 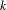 $k$-linear presentable categories which in combination of various calculations in the setting of derived algebraic geometry gives a categorical proof of the classical Atiyah–Bott formula (also known as the Holomorphic Lefschetz fixed point formula).
$k$-linear presentable categories which in combination of various calculations in the setting of derived algebraic geometry gives a categorical proof of the classical Atiyah–Bott formula (also known as the Holomorphic Lefschetz fixed point formula).
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1739 - 1763
- Copyright
- © Cambridge University Press 2018
References
- 3
- Cited by





