Research Article
Omega-Polish spaces and measurable selections
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-265
-
- Article
-
- You have access
- Export citation
Combinatorial solution of certain systems of linear equations involving (0,1) matrices
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 266-274
-
- Article
-
- You have access
- Export citation
Embedding categories with exactness into their abelianization
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 275-283
-
- Article
-
- You have access
- Export citation
A new proof of the absence of limit cycles in a quadratic autonomous system
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 284-291
-
- Article
-
- You have access
- Export citation
Note on monoidal monads
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 292-311
-
- Article
-
- You have access
- Export citation
Promonoidal functor categories
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 312-328
-
- Article
-
- You have access
- Export citation
Sylow subgroups of transitive permutation groups II
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 329-332
-
- Article
-
- You have access
- Export citation
Extensions of semi-hereditary rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 333-339
-
- Article
-
- You have access
- Export citation
Essential extensions in radical theory for rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 340-347
-
- Article
-
- You have access
- Export citation
Construction of balanced incomplete block designs
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 348-353
-
- Article
-
- You have access
- Export citation
The bichromaticity of a lattice-graph
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 354-359
-
- Article
-
- You have access
- Export citation
Free topological groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 360-365
-
- Article
-
- You have access
- Export citation
On transposes of nilpotent matrices over arbitrary rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-370
-
- Article
-
- You have access
- Export citation
Positive derivations on f-rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 371-375
-
- Article
-
- You have access
- Export citation
A discrete analogue of the Paley-Wiener theorem for bounded analytic functions in a half plane
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 376-378
-
- Article
-
- You have access
- Export citation
The Artin radical of a Noetherian ring
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 379-384
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 23 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 23 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



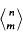 denote the least integer
denote the least integer 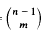 +1 for
+1 for 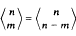 for 1 ≦ m < n.
for 1 ≦ m < n.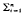 a
a be the subspace topology on the Graev group
be the subspace topology on the Graev group