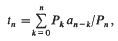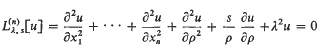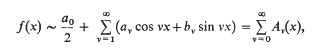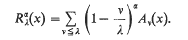Research Article
A note on commutative Baer rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-6
-
- Article
-
- You have access
- Export citation
Absolute summability of some series related to a fourier series
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-14
-
- Article
-
- You have access
- Export citation
Uniqueness of complementing pairs in partially ordered abelian groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-16
-
- Article
-
- You have access
- Export citation
Fixed points and iteration homotopies
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-20
-
- Article
-
- You have access
- Export citation
A cauchy criterion and a convergence theorem for Riemann-complete integral
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 21-24
-
- Article
-
- You have access
- Export citation
Permutational products of lattice ordered groups1
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-34
-
- Article
-
- You have access
- Export citation
Decomposition theorems for the generalized metaharmonic equation in several independent variables
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 35-46
-
- Article
-
- You have access
- Export citation
Annihilator and complemented banach*-algebras
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 47-66
-
- Article
-
- You have access
- Export citation
On the connectification of a space by a countable point set
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 67-70
-
- Article
-
- You have access
- Export citation
On typical means of fourier series of continuous functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 71-75
-
- Article
-
- You have access
- Export citation
Permutation characters
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 76-90
-
- Article
-
- You have access
- Export citation
Buckling of elastic plates by the method of constant deflection lines
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-103
-
- Article
-
- You have access
- Export citation
Formulae for absolute moments
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 104-106
-
- Article
-
- You have access
- Export citation
Multivariate semi-markov matrices
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 107-113
-
- Article
-
- You have access
- Export citation
Soluble Semigroups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 114-118
-
- Article
-
- You have access
- Export citation
On the radical of the group algebra of a p-nilpotent group
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-123
-
- Article
-
- You have access
- Export citation
The deficiency and the multiplicator of finite nilpotent groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 124-128
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 13 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 13 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation



 then
then