In this note it is proved that a BIB(ν, k, l) implies N(ν −4) ≧ min (N(k–2), N(k–1) –1, N(k)–1) and that N(69)≧6.

A classical theorem states that if a polynomial with integral coefficients is an in mth power for every integral value of its argument, then it is the mth power of a polynomial with integral coefficients.

In this paper we deal with analogous problems concerning functions which arise as solutions of recurrence equations with constant coefficients.

This paper provides explicit formulas for the Wall polynomials which arise in Wall's work on conjugacy classes in the unitary, symplectic and orthogonal groups. From these explicit formulas are easily derived six interesting limiting idetities incuding the two that arise in the Luszing-Macdonald Wall conjectures.

An (n + 1, n2 + n + 1)-packing is a collection of blocks, each of size n + 1, chosen from a set of size n2 + n + 1, such that no pair of points is contained in more than one block. If any two blocks contain a common point, then the packing can be extended to a projective plane of order n, provided the number of blocks is sufficiently large. We study packings which have a pair of disjoint blocks (such a packing clearly cannot be extended to a projective plane of order n). No such packing can contain more than n2 + n/2 blocks. Also, if n is the order of a projective plane, then we can construct such a packing with n2 + 1 blocks.

It is shown that if a1,…,am are relatively prime integers then for every integer n the equation has infinitely many solutions in pairwise relatively prime integers x1,…,xm.

Random Fourier series are studied for a class of compact abelian hypergroups. The randomizing factors are assumed to be independent and uniformly subgaussian. In the presence of a natural teachnical hypothesis, an entropy condition of Dudley is shown to be sufficient for almost sure continuity. The classical results on almost sure membership in Lp, where p < ∞, are generalized to this setting. As an application, it is shown that a simple condition on the dual object implies that the de Leeuw-Kahane-Katznelson phenomenon occurs. Another application is the analogue of a classical sufficient condition for almost sure continuity. Examples illustrating the general theory are given for the hypergroup of conjugacy classes of SU(2) and for a class of compact countable hypergroups.

Defining a function on the set of all Riemannian metrics associated to a contact form on a compact manifold by taking the integral of the Ricci curvature in the direction of the characteristic vector field, it is shown that on a compact regular contact manifold the only critical points of this function are the metrics for which the characteristic vector field generates a group of isometrics.

In an earlier paper we showed that the set ψ+ (X, Y) of super Tauberian transformations between two Banach spaces X and Y forms an open subset of B(X, Y) which is closed under perturbation by super weakly compact transformations. In this note we characterize a class dual to ψ+ (X, Y) which we denote by ψ-(X, Y). We show that T∈ψ+(X, Y) if and only if T′ ∈ ψ-(Y′, X′) and that T′∈ψ+(Y′, X′) if and only if T ∈ ψ-(X, Y) and provide standard and nonstandard characterizations of elements of ψ-(X, Y). These two classes thus play in some ways analogous roles to the sets of semi-Fredholm transforms ϕ+ (X, Y) and ϕ-(X, Y).

Moreover 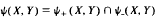en forms an open subset of B(X, Y) closed under the taking of adjoints, under the taking of nonstandard hull extensions, and under perturbation by super weakly compact transformations.

Different methods are used to show that a finite or countable product of Lindelöf scattered spaces is Lindelöf. Also, a technique of Kunen is modified to yield results concerning the Lindelöf degree of the Gδ and Gα-topologies on the countable product of compact scattered spaces.

A space X is said to be D1 provided each closed set has a countable basis for the open sets containing it. It is said to be D2 provided there is a countable base {Un} such that each closed set has a countable base for the open sets containing it, which is a subfamily of {Un}. In this paper, we give a separation theorem for D1 spaces, and provide a characterization of D1 and D2 spaces in terms of maps.

Let A be an Archimedean, uniformly complete, semiprime f-algebra and F(X1,…Xn) ∈ R+ [X1,…Xn] a homogeneous polynomial of degree p (p∈ N). It is shown that (F(u 1…unn))1/p exists in A+ for all u1…un ∈ A+.

Let S(m, M) be the set of functions regular and satisfying │zf′(z)/f(z) – m│< M in │z│ <1, where│m –│ <M;≦ m; and let S*(p) be the set of starlike functions of order p, 0≦ p <1. In this paper we obtain integral operators which map S(m, M) into S(mM) and S* (p) × S(mM) into S*(p). Our results improve and generalize many recent results.

An operator form of the Euler-Maclaurin sum formula is obtained, expressing the sum of the Euler-Maclaurin infinite series in a closed derivation, whose spectrum is compact, not equal to {0}, and does not have 0 as a clusterpoint, as the difference between a summation operator and an antiderivation which is the local inverse of the derivation.

It is shown that a positive measure μ on the Borel subsets of Rk is translation-bounded if and only if the Fourier transform of the indicator function of every bounded Borel subset of Rk belongs to L2(μ).