Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-26T11:33:50.921Z Has data issue: false hasContentIssue false
  • English
  • Français

The stability of harrod's growth model of an economy

Published online by Cambridge University Press:  09 April 2009

P. E. Lush
P. E. Lush
Affiliation:
University of New England, Armidale.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Nevile [2] has shown that if Rt is a certain measure of the rate of growth of the national income in Harrod's growth model of an economy, then Rt satisfies the non-linear recurrence relation 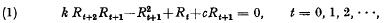, where 0 < k < and −1 < c < 1. The definition of Rt ([2] p. 369) is such that Rt > 0 for all t. Nevile has pointed out features of the model that indicate that it may be unstable. In this paper I propose to show that the model is, in general. unstable, but that proper choice of the initial values R0R1 apparently leads to stability. In order to do this, we require the conditions (if any) under which Rt converges.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 5 , Issue 2 , May 1965 , pp. 207 - 215
Copyright
Copyright © Australian Mathematical Society 1965

References

[1]Chaundy, T. W. and Phillips, E., The convergence of sequences defined by quadratic recurrence-formulae, Quart J. of Math. (Oxford) 7 (1936), 74–80.CrossRefGoogle Scholar
[2]Nevile, J. W., The mathematical formulation of Harrod's growth model, Econ. J. 72 (1962), 367–370.Google Scholar
[3]Kuczma, M., On monotonic solutions of a functional equation I, Ann. Polon. Math. 9 (1960), 295–297.CrossRefGoogle Scholar
[4]Kuczma, M., On monotonic solutions of a functional equation II, Ann. Polon. Math. 10 (1961), 161–166.CrossRefGoogle Scholar
[5]Fort, M. K., Continuous solutions of a functional equation, Ann. Polon. Math. 13 (1963), 205–211.CrossRefGoogle Scholar
[6]Panov, A. M., The behaviour of the solutions of difference equations near a fixed point, Izv. Vyss. Ucebn. Zaved. Matematika (1959), no. 5 (19), 174–183. (Russian).Google Scholar
[7]Choczewski, B., On continuous solutions of some functional equations of the n-th order, Ann. Polon. Math. 11 (1961), 123–132.CrossRefGoogle Scholar