Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-17T13:59:36.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Quotient groups and realization of tight Riesz groups

Published online by Cambridge University Press:  09 April 2009

John Boris Miller
John Boris Miller
Affiliation:
Monash University Clayton, 3168 Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (G, ≼) be an l-group having a compatible tight Riesz order ≦ with open-interval topology U, and H a normal subgroup. The first part of the paper concerns the question: Under what conditions on H is the structure of (G, ≼, ∧, ∨, ≦, U) carried over satisfactorily to 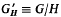by the canonical homomorphism; and its answer (Theorem 8°): H should be an l-ideal of (G, ≼) closed and not open in (G, U). Such a normal subgroup is here called a tangent. An essential step is to show that ≼′ is the associated order of ≦′.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 16 , Issue 4 , December 1973 , pp. 416 - 430
Copyright
Copyright © Australian Mathematical Society 1973

References

[1]Cameron, Neil & Miller, J. B., Topology and axioms of interpolation in partially ordered spaces (J. für die reine u. angew. Math., to appear).Google Scholar
[2]Fuchs, L., Partially ordered algebraic systems (Pergamon, Oxford, 1963).Google Scholar
[3]Fuchs, L., ‘Riesz groups’, Ann. Scuola Norm. Sup. Pisa 19 (1965), 1–34.Google Scholar
[4]Loy, R. J. & Miller, J. B., ‘Tight Riesz groups’, J. Austral. Math. Soc. 13 (1972), 224–240.CrossRefGoogle Scholar
[5]Miller, J. B., ‘Higher derivations on Banach algebras’, Amer. J. Math. 92 (1970), 301–331.CrossRefGoogle Scholar
[6]Miller, J. B., ‘Tight Riesz groups and the Stone-Weierstrass theorem’ (Preprint, Monash University, 1970).Google Scholar
[7]Reilly, N. R., Compatible tight Riesz orders and prime subgroups. (Preprint, Simon Fraser University, 1971).Google Scholar
[8]Ribenboim, P., Théorie des groupes ordonnés (Universidad Nacional del Sur, Bahia Blanca, 1959).Google Scholar
[9]Speed, T. P. & Strzelecki, E., ‘A note on commutative l-groups’, J. Austral. Math. Soc. 12 (1971), 69–74.CrossRefGoogle Scholar
[10]Spirason, G. T. & Strzelecki, E., ‘A note on Pt-ideals’, J. Austral. Math. Soc. 14 (1972), 304–310.CrossRefGoogle Scholar
[11]Wirth, A., ‘Compatible tight Riesz orders’, J. Austral. Math. Soc. 15 (1973), 105–111.CrossRefGoogle Scholar