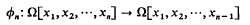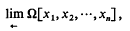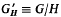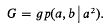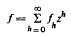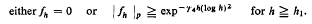Research Article
The SQ-universality of some finitely presented groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-6
-
- Article
-
- You have access
- Export citation
The inverse limit of some free algebras
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-145
-
- Article
-
- You have access
- Export citation
A note on BIBD's
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-261
-
- Article
-
- You have access
- Export citation
The hulls of representable l-groups and f-rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-415
-
- Article
-
- You have access
- Export citation
Quotient groups and realization of tight Riesz groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 416-430
-
- Article
-
- You have access
- Export citation
I-Subsemigroups and α-monomorphisms
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 146-166
-
- Article
-
- You have access
- Export citation
A construction of rings whose injective hulls allow a ring structure
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 7-13
-
- Article
-
- You have access
- Export citation
The nullity of a wild knot in a compact 3-manifold
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 262-271
-
- Article
-
- You have access
- Export citation
Lipschitz conditions and lacunarity
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 272-277
-
- Article
-
- You have access
- Export citation
A class of modules over a locally finite group I
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 431-442
-
- Article
-
- You have access
- Export citation
Negative curvature and combinatorial group theory
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 14-15
-
- Article
-
- You have access
- Export citation
On one-factorizations of complete graphs
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 167-171
-
- Article
-
- You have access
- Export citation
Free inverse semigroups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 443-453
-
- Article
-
- You have access
- Export citation
Isomorphisms induced by automorphisms
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-17
-
- Article
-
- You have access
- Export citation
The soluble subgroups of a one-relator group with torsion
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 278-285
-
- Article
-
- You have access
- Export citation
On duality in complex linear programming
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 172-175
-
- Article
-
- You have access
- Export citation
The third term of the lower central series of a free group as a subgroup of the second
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-23
-
- Article
-
- You have access
- Export citation
A p-adic analogue to a theorem by J. Popken
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 176-184
-
- Article
-
- You have access
- Export citation
Asymptotically quasi-compact products of bounded linear operators
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 286-289
-
- Article
-
- You have access
- Export citation
Two notes on Rankin's book on the modular group
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 454-457
-
- Article
-
- You have access
- Export citation