Let k be a fixed integer ≧2. A positive integer n is called unitarily k-free, if the multiplicity of each prime divisor of n is not a multiple of k; or equivalently, if n is not divisible unitarily by the kth power of any integer > 1. By a unitary divisor, we mean as usual a divisor d > 0 of n such that (d,(n/d)) = 1. The integer 1 is also considered to be unitarily k-free. These integers were first defined by Cohen (1961; § 1). Let Q*k denote the set of unitarily k-free integers. When k = 2, the set Q*2 coincides with the set Q* of exponentially odd integers (that is, integers in whose canonical representation each exponent is odd) discussed by Cohen himself in an earlier paper (1961; § 1 and § 6). Let x denote a real variable 1 and let Q*k denote the number of unitarily k-free integers ≦ x. Cohen (1961; Theorem 3.2) established by purely elementary methods that 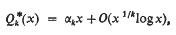, where 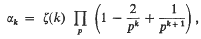, the product being extended over all primes p and ζ(k) denotes the Riemann Zeta function. In the same paper Cohen (1961; Theorem 4.2) improved the order estimate of the error term in (1.1) to O(x1/k), by making use of the properties of real Dirichiet series. Later, he (Cohen; 1964) proved the same result by purely elementary methods eliminating the use of Dirichlet series.