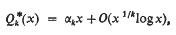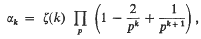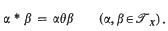Research Article
Distribution of unitarily k-free integers
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-141
-
- Article
-
- You have access
- Export citation
Left invariant measure in topological semigroups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 142-145
-
- Article
-
- You have access
- Export citation
Recursive density types and Nerode extensions of arithmetic
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 146-158
-
- Article
-
- You have access
- Export citation
Generators of reflexive algebras
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-164
-
- Article
-
- You have access
- Export citation
A multifunction generalization of Gale's Ascoli theorem
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-171
-
- Article
-
- You have access
- Export citation
Semigroups in rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 172-177
-
- Article
-
- You have access
- Export citation
On p-groups with a cyclic commutator subgroup
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 178-198
-
- Article
-
- You have access
- Export citation
Some groups of Fibonacci type
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-204
-
- Article
-
- You have access
- Export citation
Note on operations generating the group operations in nilpotent groups of class 3
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 205-206
-
- Article
-
- You have access
- Export citation
Projectively torsion-free modules
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 207-221
-
- Article
-
- You have access
- Export citation
Embedding a semigroup of transformations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 222-224
-
- Article
-
- You have access
- Export citation
Growth sequences of finite groups II
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 225-229
-
- Article
-
- You have access
- Export citation
Estimation of Partial derivatives of the average of densities belonging to a family of densities
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 230-241
-
- Article
-
- You have access
- Export citation
A note on linear recursive sequences
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 242-244
-
- Article
-
- You have access
- Export citation
Notes on differential calculus in topological linear spaces, II
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 245-252
-
- Article
-
- You have access
- Export citation
Groups with an automorphism cubing many elements
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-256
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 20 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 20 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation