Research Article
Determinateness of certain almost-Borel games
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 569-579
-
- Article
- Export citation
On the number of generators of cylindric algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 865-873
-
- Article
- Export citation
Global quantification in Zermelo-Fraenkel set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 289-301
-
- Article
- Export citation
Automorphisms of supermaximal subspaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-9
-
- Article
- Export citation
On the structure of Ext(A,Z) in ZFC+
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 302-315
-
- Article
- Export citation
On the T-degrees of partial functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 580-588
-
- Article
- Export citation
Some results concerning strongly compact cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 874-880
-
- Article
- Export citation
Fibered categories and the foundations of naive category theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 10-37
-
- Article
- Export citation
A consistent prepositional logic without any finite models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 38-41
-
- Article
- Export citation
Nonsplitting subset of
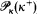 κ(κ+)
κ(κ+)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 881-894
-
- Article
- Export citation
Extension of relatively σ-additive probabilities on Boolean algebras of logic1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 589-596
-
- Article
- Export citation
Quelques précisions sur la D.O.P. et la profondeur d'une théorie
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 316-330
-
- Article
- Export citation
Epistemic set theory is a conservative extension of intuitionistic set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 895-902
-
- Article
- Export citation
Vopěnka's principle and compact logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 42-48
-
- Article
- Export citation
Two weak consequences of 0#
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 597-603
-
- Article
- Export citation
Functors and ordinal notations. IV: The Howard ordinal and the functor ∧.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 331-338
-
- Article
- Export citation
A recursive model for arithmetic with weak induction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 49-54
-
- Article
- Export citation
Finitely generic models of TUH, for certain model companionable theories T
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 604-610
-
- Article
- Export citation
A direct proof of the finite developments theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 339-343
-
- Article
- Export citation
The completeness of a predicate-functor logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 903-926
-
- Article
- Export citation

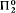 ,
, 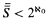 , and the game whose winning set is
, and the game whose winning set is 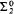 sets and sets smaller than the continuum.
sets and sets smaller than the continuum.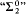 is replaced by “Borel”.
is replaced by “Borel”.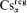 and Cs
and Cs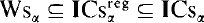 ⊆ CA
⊆ CA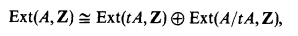

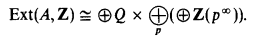
 and ν
and ν , ≤ 〉 be the usual structure of the degrees of unsolvability and 〈
, ≤ 〉 be the usual structure of the degrees of unsolvability and 〈 , ≤ 〉 the structure of the
, ≤ 〉 the structure of the  . If also
. If also 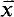 denotes its order type in the natural ordering. The identity function with the domain appropriate to the context is denoted by id. For the notation concerning ultrapowers and elementary embeddings, see [11]. When we talk about forcing, “⊩” will mean “weakly forces” and “
denotes its order type in the natural ordering. The identity function with the domain appropriate to the context is denoted by id. For the notation concerning ultrapowers and elementary embeddings, see [11]. When we talk about forcing, “⊩” will mean “weakly forces” and “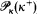
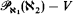 stationary
stationary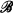 . Second, in a fashion completely analogous to the construction of Boolean-valued models of classical set theory, we define the
. Second, in a fashion completely analogous to the construction of Boolean-valued models of classical set theory, we define the 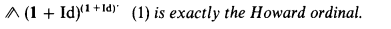
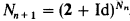 , but we are incapable of expressing SYN(
, but we are incapable of expressing SYN(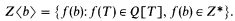
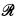 be a set of occurrences of redexes in
be a set of occurrences of redexes in