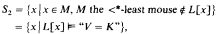Research Article
Recursion in Kolmogorov's R-operator and the ordinal σ3
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-11
-
- Article
- Export citation
Partitions and filters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 12-21
-
- Article
- Export citation
research-article
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 22-32
-
- Article
- Export citation
Weak partition relations and measurability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 33-38
-
- Article
- Export citation
0# and some forcing principles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 39-46
-
- Article
- Export citation
Jensen's ⃞ principles and the Novák number of partially ordered sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 47-58
-
- Article
- Export citation
Locally finite theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 59-62
-
- Article
- Export citation
Omitting types in
 -minimal theories
-minimal theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 63-74
-
- Article
- Export citation
Tarski's problem for varieties of groups with a commutator identity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 75-78
-
- Article
- Export citation
Decision problems concerning properties of finite sets of equations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 79-87
-
- Article
- Export citation
Splitting properties of r.e. sets and degrees1,2
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 88-109
-
- Article
- Export citation
The index set {e: We ≡1X}.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 110-116
-
- Article
- Export citation
Pairs without infimum in the recursively enumerable weak truth table degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 117-129
-
- Article
- Export citation
The natural hierarchy and quasi-hierarchy of constructibility degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 130-134
-
- Article
- Export citation
Elementary equivalence of Cσ(K) spaces for totally disconnected, compact Hausdorff K
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 135-146
-
- Article
- Export citation
Stationary reflections for uncountable cofinality
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 147-151
-
- Article
- Export citation
Finitely generated free Heyting algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 152-165
-
- Article
- Export citation
Intuitionistic tense and modal logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 166-179
-
- Article
- Export citation
On the intersection of closed unbounded sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 180-189
-
- Article
- Export citation
Axioms of symmetry: Throwing darts at the real number line
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 190-200
-
- Article
- Export citation

 = the set of partial functions from
= the set of partial functions from 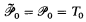
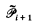 = the set of consistent partial functions from
= the set of consistent partial functions from 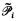 to
to 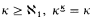 , then
, then  principle, show by forcing that it is consistent and use it to construct an ℵ
principle, show by forcing that it is consistent and use it to construct an ℵ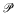 such that the game of length
such that the game of length 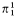 -indescribable) and elementary properties of the constructible hierarchy are used. For this and all undefined terms we refer the reader to Jech [10].
-indescribable) and elementary properties of the constructible hierarchy are used. For this and all undefined terms we refer the reader to Jech [10]. -minimal theories
-minimal theories
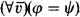 , where
, where  -complete, answering a question posed by Odifreddi in [2].
-complete, answering a question posed by Odifreddi in [2].