Other
Survey/expository papers
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 865
-
- Article
- Export citation
Alfred Tarski
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 866-868
-
- Article
- Export citation
Research Article
Alfred Tarski's work in model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 869-882
-
- Article
- Export citation
The contributions of Alfred Tarski to general algebra
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 883-889
-
- Article
- Export citation
Alfred Tarski and undecidable theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 890-898
-
- Article
- Export citation
The contributions of Alfred Tarski to algebraic logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 899-906
-
- Article
- Export citation
Tarski and geometry
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 907-912
-
- Article
- Export citation
Other
Bibliography of Alfred Tarski
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 913-941
-
- Article
- Export citation
Research Article
A boundedness theorem in ID1(W)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 942-947
-
- Article
- Export citation
Sur la théorie élémentaire des corps de fonctions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 948-956
-
- Article
- Export citation
Why Solovay real produces Cohen real
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 957-968
-
- Article
- Export citation
Back and forth constructions in modal logic: An interpolation theorem for a family of modal logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 969-980
-
- Article
- Export citation
Transfer principles for pseudo real closed e-fold ordered fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 981-991
-
- Article
- Export citation
Axioms for the set-theoretic hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 992-1004
-
- Article
- Export citation
Conservative extensions of models of set theory and generalizations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1005-1021
-
- Article
- Export citation
Preservation theorem and relativization theorem for cofinal extensions1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1022-1028
-
- Article
- Export citation
The weak □* is really weaker than the full □
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1029-1033
-
- Article
- Export citation
Degrees coded in jumps of orderings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1034-1042
-
- Article
- Export citation
Bad models in nice neighborhoods
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1043-1055
-
- Article
- Export citation
On a combinatorial principle of Hajnal and Komjáth
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1056-1060
-
- Article
- Export citation

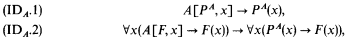
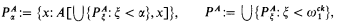
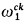 is the first nonrecursive ordinal.
is the first nonrecursive ordinal.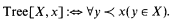
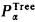 , respectively. Since
, respectively. Since 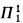 complete we have
complete we have 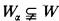 for all α <
for all α < 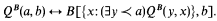
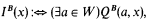
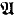 be an arbitrary model of set theory. Does there exist an elementary extension
be an arbitrary model of set theory. Does there exist an elementary extension 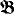 of
of 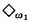 in [RS], and already employed in [E1], we prove that our question in general has a negative answer (see Theorem 2.3). This result generalizes the results of M. Kaufmann and the author (appearing respectively in [Ka] and [E1]) concerning models of set theory with no elementary end extensions.
in [RS], and already employed in [E1], we prove that our question in general has a negative answer (see Theorem 2.3). This result generalizes the results of M. Kaufmann and the author (appearing respectively in [Ka] and [E1]) concerning models of set theory with no elementary end extensions.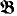 of an
of an 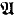 is said to be an outer extension of
is said to be an outer extension of 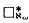 does not imply
does not imply 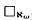 . The model-theoretic transfer property ⟨ℵ
. The model-theoretic transfer property ⟨ℵ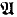 is a structure, then
is a structure, then 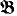 be the copy of
be the copy of 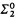 .
.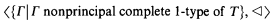
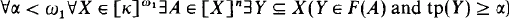 .
.