Research Article
An α-finite injury method of the unbounded type1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-17
-
- Article
- Export citation
The unprovability in intuitionistic formal systems of the continuity of effective operations on the reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 18-24
-
- Article
- Export citation
Omitting types in set theory and arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 25-32
-
- Article
- Export citation
Infinitary compactness without strong inaccessibility1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 33-38
-
- Article
- Export citation
Two variable implicational calculi of prescribed many-one degrees of unsolvability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 39-44
-
- Article
- Export citation
A reduction class containing formulas with one monadic predicate and one binary function symbol
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 45-49
-
- Article
- Export citation
Probabilities on finite models1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 50-58
-
- Article
- Export citation
Approximation theorems and model theoretic forcing
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 59-72
-
- Article
- Export citation
One more aspect of forcing and omitting types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 73-80
-
- Article
- Export citation
Completeness properties of heyting's predicate calculus with respect to re models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 81-94
-
- Article
- Export citation
Negative-existentially complete structures and definability in free extensions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 95-108
-
- Article
- Export citation
Uniform inductive definability and infinitary languages
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 109-120
-
- Article
- Export citation
Semantics of the infinitistic rules of proof
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 121-138
-
- Article
- Export citation
Elementary extensions of countable models of set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 139-145
-
- Article
- Export citation
Ed-regressive sets of order n
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 146-152
-
- Article
- Export citation
Selection in abstract recursion theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 153-158
-
- Article
- Export citation
An intuitiomstic completeness theorem for intuitionistic predicate logic1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 159-166
-
- Article
- Export citation
On Σ1 well-orderings of the universe
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 167-170
-
- Article
- Export citation
Applications of vaught sentences and the covering theorem1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 171-187
-
- Article
- Export citation
Monotone inductive definitions over the continuum
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 188-198
-
- Article
- Export citation

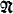 = ω, +, ·, < and complete with respect to Th(
= ω, +, ·, < and complete with respect to Th(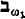 so the condition will be called
so the condition will be called 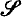 be a finite set of (nonlogical) predicate symbols. By an
be a finite set of (nonlogical) predicate symbols. By an 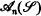 be the set of all
be the set of all 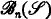 be a subset of
be a subset of 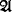 in
in 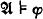 and
and 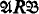 imply
imply 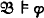 ) iff there exists φ* ϵ Φ such that ⊧
) iff there exists φ* ϵ Φ such that ⊧ of models of
of models of 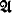 , such that φ(
, such that φ(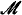 arising from the theory of inductive definability, and uniformly Σ
arising from the theory of inductive definability, and uniformly Σ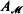 . The structures we have in mind are called
. The structures we have in mind are called 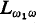 . On the other hand the study of representability in second order arithmetic with the ω-rule added revealed for the first time an analogy between the notions of re-cursivity and hyperarithmeticity which had an important influence on the further development of generalized recursion theory.
. On the other hand the study of representability in second order arithmetic with the ω-rule added revealed for the first time an analogy between the notions of re-cursivity and hyperarithmeticity which had an important influence on the further development of generalized recursion theory.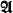 is a countable model of ZFC and
is a countable model of ZFC and 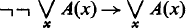
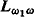 . Among others, we prove that if every countable model in a PC
. Among others, we prove that if every countable model in a PC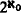 nonisomorphic countable members (cf. Theorem 4.3*) and that the class of countable saturated structures of a sufficiently large countable similarity type is not
nonisomorphic countable members (cf. Theorem 4.3*) and that the class of countable saturated structures of a sufficiently large countable similarity type is not 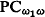 among countable structures (cf. Theorem 5.2). We also give a simple proof of the Lachlan-Sacks theorem on bounds of Morley ranks (§7).
among countable structures (cf. Theorem 5.2). We also give a simple proof of the Lachlan-Sacks theorem on bounds of Morley ranks (§7).