Errata
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. viii
-
- Article
-
- You have access
- Export citation
A Survey/expository paper
The roots of contemporary Platonism
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1121-1144
-
- Article
- Export citation
Research Article
Coding over a measurable cardinal
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1145-1159
-
- Article
- Export citation
On hyper-torre isols
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1160-1166
-
- Article
- Export citation
Descriptive set theory over hyperfinite sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1167-1180
-
- Article
- Export citation
Near-equational and equational systems of logic for partial functions. II1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1181-1215
-
- Article
- Export citation
The formal language of recursion
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1216-1252
-
- Article
- Export citation
Definability in terms of the successor function and the coprimeness predicate in the set of arbitrary integers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1253-1287
-
- Article
- Export citation
Recursively enumerable sets modulo iterated jumps and extensions of Arslanov's completeness criterion
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1288-1323
-
- Article
- Export citation
Some restrictions on simple fixed points of the integers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1324-1345
-
- Article
- Export citation
A proof of morley's conjecture
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1346-1358
-
- Article
- Export citation
The classification of excellent classes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1359-1381
-
- Article
- Export citation
Large resplendent models generated by indiscernibles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1382-1388
-
- Article
- Export citation
Algorithmic information theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1389-1400
-
- Article
- Export citation
The consistency problem for positive comprehension principles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1401-1418
-
- Article
- Export citation
Interpolation in fragments of intuitionistic propositional logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1419-1430
-
- Article
- Export citation
The number of pairwise non-elementarily-embeddable models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1431-1455
-
- Article
- Export citation
The equivalence of the disjunction and existence properties for modal arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1456-1459
-
- Article
- Export citation
A general treatment of equivalent modalities
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1460-1471
-
- Article
- Export citation
Reviews
Robert Bull and Krister Segerberg. Basic modal logic. Handbook of philosophical logic, Volume II, Extensions of classical logic , edited by D. Gabbay and F. Guenthner, Synthese library, vol. 165, D. Reidel Publishing Company, Dordrecht, Boston, and Lancaster, 1984, pp. 1–88. - John P. Burgess. Basic tense logic. Handbook of philosophical logic, Volume II, Extensions of classical logic , edited by D. Gabbay and F. Guenthner, Synthese library, vol. 165, D. Reidel Publishing Company, Dordrecht, Boston, and Lancaster, 1984, pp. 89–133. - Richmond H. Thomason. Combinations of tense and modality. Handbook of philosophical logic, Volume II, Extensions of classical logic , edited by D. Gabbay and F. Guenthner, Synthese library, vol. 165, D. Reidel Publishing Company, Dordrecht, Boston, and Lancaster, 1984, pp. 135–165. - Johan van Benthem. Correspondence theory. Handbook of philosophical logic, Volume II, Extensions of classical logic , edited by D. Gabbay and F. Guenthner, Synthese library, vol. 165, D. Reidel Publishing Company, Dordrecht, Boston, and Lancaster, 1984, pp. 167–247. - James W. Garson. Quantification in modal logic. Handbook of philosophical logic, Volume II, Extensions of classical logic , edited by D. Gabbay and F. Guenthner, Synthese library, vol. 165, D. Reidel Publishing Company, Dordrecht, Boston, and Lancaster, 1984, pp. 249–307. - Nino B. Cocchiarella. Philosophical perspectives on quantification in tense and modal logic. Handbook of philosophical logic, Volume II, Extensions of classical logic , edited by D. Gabbay and F. Guenthner, Synthese library, vol. 165, D. Reidel Publishing Company, Dordrecht, Boston, and Lancaster, 1984, pp. 309–353.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1472-1477
-
- Article
- Export citation

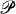 for producing a real R such that
for producing a real R such that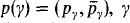 belonging to an initial segment of the cardinals, where
belonging to an initial segment of the cardinals, where 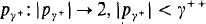 into a subset of
into a subset of 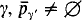 for only a
for only a 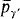 and the need to code extensions of
and the need to code extensions of 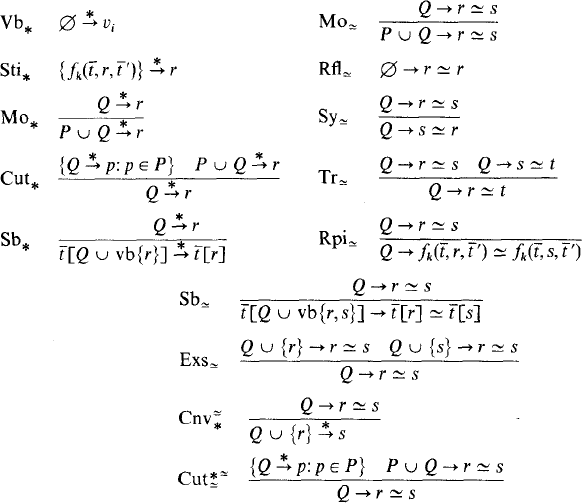
 where
where  is countable. Although excellence arises in the study of the model theory of Scott sentences, it is not a dividing line in a classification of them. In particular, the assumption of nonexcellence does not yield much information. In fact, in [3] there is an example of a nonexcellent Scott sentence, categorical in ℵ
is countable. Although excellence arises in the study of the model theory of Scott sentences, it is not a dividing line in a classification of them. In particular, the assumption of nonexcellence does not yield much information. In fact, in [3] there is an example of a nonexcellent Scott sentence, categorical in ℵ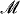 is a countable, recursively saturated model of PA, then for each infinite cardinal κ there is a resplendent
is a countable, recursively saturated model of PA, then for each infinite cardinal κ there is a resplendent 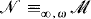 which has cardinality κ
which has cardinality κ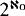 normal logics, and since one immediately realizes that there are infinitely many m-partitions, the problem consists in choosing (assuming the continuum hypothesis) between ℵ
normal logics, and since one immediately realizes that there are infinitely many m-partitions, the problem consists in choosing (assuming the continuum hypothesis) between ℵ