Research Article
Simplified morasses with linear limits
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1001-1021
-
- Article
- Export citation
Diamonds, uniformization
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1022-1033
-
- Article
- Export citation
More on proper forcing
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1034-1038
-
- Article
- Export citation
The strength of nonstandard methods in arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1039-1058
-
- Article
- Export citation
The undecidability of entailment and relevant implication
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1059-1073
-
- Article
- Export citation
Typical ambiguity and the axiom of choice
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1074-1078
-
- Article
- Export citation
Functors and ordinal notations. II: A functorial construction of the Bachmann hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1079-1114
-
- Article
- Export citation
The model theory of finitely generated finite-by-abelian groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1115-1124
-
- Article
- Export citation
The universal complementation property
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1125-1136
-
- Article
- Export citation
Decidable subspaces and recursively enumerable subspaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1137-1145
-
- Article
- Export citation
Bases of supermaximal subspaces and Steinitz systems. I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1146-1159
-
- Article
- Export citation
A hierarchy of families of recursively enumerable degrees12
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1160-1170
-
- Article
- Export citation
The uniqueness of envelopes in ℵ0-categorical, ℵ0-stable structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1171-1184
-
- Article
- Export citation
Forcing the failure of CH by adding a real
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1185-1189
-
- Article
- Export citation
Definable structures in the lattice of recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1190-1197
-
- Article
- Export citation
The consistency strength of the free-subset property for ωω
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1198-1204
-
- Article
- Export citation
Pseudo-jump operators. II: Transfinite iterations, hierarchies and minimal covers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1205-1236
-
- Article
- Export citation
The unsolvability of the Gödel class with identity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1237-1252
-
- Article
- Export citation
A decidable subclass of the minimal Gödel class with identity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1253-1261
-
- Article
- Export citation
A normal form theorem for first order formulas and its application to Gaifman's splitting theorem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1262-1267
-
- Article
- Export citation

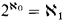 ,
, 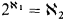 ,
, 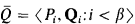
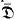 -
-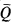
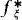 :
: 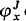 of functors from
of functors from 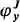 ; we show that, if the garden is
; we show that, if the garden is 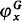 coincides exactly with the usual hierarchy
coincides exactly with the usual hierarchy 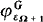 (0) is the usual Howard ordinal. We show also, that for eac
(0) is the usual Howard ordinal. We show also, that for eac 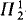 -
-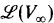 of recursively enumerable subspaces has been extensively studied since its introduction by Metakides and Nerode [MN1] (see for example, [Do2], [Gu], [KR], [Re1], [Re2], and [Sh]). For those unfamiliar with the literature on
of recursively enumerable subspaces has been extensively studied since its introduction by Metakides and Nerode [MN1] (see for example, [Do2], [Gu], [KR], [Re1], [Re2], and [Sh]). For those unfamiliar with the literature on 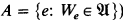 of recursively enumerable sets such that
of recursively enumerable sets such that 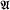 and if
and if 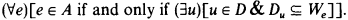
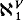 =
= 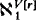 .
.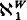 =
= 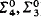 ), i.e. isomorphic to the lattice of
), i.e. isomorphic to the lattice of 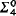 sets together with a unary predicate selecting out exactly the
sets together with a unary predicate selecting out exactly the 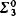 sets.
sets.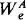 for some index
for some index 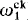 and Kleene's hyperarithmetic hierarchy. The REA sets will then, of course, be the results of applying these operators to the empty set. They will extend and generalize Kleene's
and Kleene's hyperarithmetic hierarchy. The REA sets will then, of course, be the results of applying these operators to the empty set. They will extend and generalize Kleene's 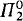 set singletons thus providing us with a new richer subclass of the
set singletons thus providing us with a new richer subclass of the 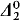 operators and so give a new hierarchy for them as well as the
operators and so give a new hierarchy for them as well as the 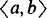 and a witness for
and a witness for 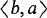 . The formulas we consider demand less: they require, for any elements a and
. The formulas we consider demand less: they require, for any elements a and