Research Article
Upward directedness of the Rudin-Keisler ordering of p-points
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 449-456
-
- Article
- Export citation
On the existence of large p-ideals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 457-465
-
- Article
- Export citation
Universal structures in power ℵ1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 466-477
-
- Article
- Export citation
Tores et p-groupes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 478-491
-
- Article
- Export citation
Successors of singular cardinals and measurability revisited
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 492-501
-
- Article
- Export citation
The equivalence of determinacy and iterated sharps
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 502-525
-
- Article
- Export citation
Some results on higher Suslin trees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 526-536
-
- Article
- Export citation
On the quasi-ordering of Borel linear orders under embeddability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 537-560
-
- Article
- Export citation
Operative vs. combinatory spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 561-572
-
- Article
- Export citation
The ordertype of β-R.E. sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 573-576
-
- Article
- Export citation
Weak cylindric set algebras and weak subdirect indecomposability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 577-588
-
- Article
- Export citation
Taxonomies of model-theoretically defined topological properties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 589-603
-
- Article
- Export citation
Some results about Borel sets in descriptive set theory of hyperfinite sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 604-614
-
- Article
- Export citation
The deduction theorem for quantum logic—some negative results
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 615-625
-
- Article
- Export citation
The spectrum of resplendency
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 626-636
-
- Article
- Export citation
Weakly semirecursive sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 637-644
-
- Article
- Export citation
Definitions of compact
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 645-655
-
- Article
- Export citation
Some improvements to Turner's algorithm for bracket abstraction
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 656-669
-
- Article
- Export citation
The last word on elimination of quantifiers in modules
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 670-673
-
- Article
- Export citation
Finite support iteration and strong measure zero sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 674-677
-
- Article
- Export citation

 (
(
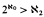 and there is a universal model of cardinality ℵ
and there is a universal model of cardinality ℵ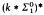 and
and 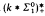 , which lie strictly between
, which lie strictly between 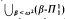 and
and 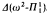 . We also define 0
. We also define 0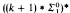 as well as the determinacy of
as well as the determinacy of  of topological spaces; and (2) a “taxonomy”, i.e. a list of first order sentences, together with a way of assigning an abstract class of spaces to each sentence of the list so that logically equivalent sentences are assigned the same class.
of topological spaces; and (2) a “taxonomy”, i.e. a list of first order sentences, together with a way of assigning an abstract class of spaces to each sentence of the list so that logically equivalent sentences are assigned the same class.