Research Article
Transcendence of cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-7
-
- Article
- Export citation
A generalization of Nelson's algorithm for obtaining prime implicants
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 8-12
-
- Article
- Export citation
Satisfaction for n-th order languages defined in n-th order languages
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 13-25
-
- Article
- Export citation
Modus ponens under hypotheses
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 26
-
- Article
- Export citation
An incorrect theorem1
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 27
-
- Article
- Export citation
Limiting recursion
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 28-48
-
- Article
- Export citation
Trial and error predicates and the solution to a problem of Mostowski*
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 49-57
-
- Article
- Export citation
An algebraic study of Diodorean modal systems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 58-64
-
- Article
- Export citation
On the logic of incomplete answers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 65-68
-
- Article
- Export citation
On the notational independence of various hierarchies of degrees of unsolvability1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 69-86
-
- Article
- Export citation
Reviews
Milton Fisk. A modern formal logic. Prentice-Hall fundamentals of logic series. Prentice-Hall, Inc., Englewood Cliffs, N.J., 1964, xi + 116 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 87-88
-
- Article
- Export citation
Raymond M. Smullyan. Theory of formal systems. Annals of Mathematics studies, no. 47. Princeton University Press, Princeton1961, xi + 142 pp. - Raymond M. Smullyan. Theory of formal systems. Revised edition. Annals of Mathematics studies, no. 47. Princeton University Press, Princeton1961, xi + 147 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 88-90
-
- Article
- Export citation
A. A. Mučnik. Réšénié problémy svodimosti Posta i nékotoryh drugih problém téorii algorifmou. I. (Solution of Post's reduction problem and of certain other problems in the theory of algorithms. I.) Trudy Moskovskogo Matématičéskogo Obščéstva, vol. 7 (1958), pp. 391–405.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 90
-
- Article
- Export citation
Paul Axt. Enumeration and the Grzegorczyk hierarchy. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, Bd. 9 (1963), S. 53–65.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 90-91
-
- Article
- Export citation
Jean Ladrière. Expression de la récursion primitive dans le calcul-λ-K. Logique et analyse, n.s. vol. 4 (1961), pp. 23–54.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 91-94
-
- Article
- Export citation
Charles Parsons. The ω-consistency of ramified analysis. Archiv für mathematische Logik und Grundlagenforschung, vol. 6 nos. 1–2 (1962), pp. 30–34.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 94
-
- Article
- Export citation
A. Tarski. Remarks on predicate logic with infinitely long expressions. Colloquium mathematicum, vol. 6 (1958), pp. 171–176. - Alfred Tarski. Remarks on predicate logic with infinitely long expressions. Summaries of talks presented at the Summer Institute for Symbolic Logic, Cornell University, 1957, 2nd edn., Communications Research Division, Institute for Defense Analyses, Princeton, N.J., 1960, pp. 160–163.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 94-95
-
- Article
- Export citation
D. Scott and A. Tarski. The sentential calculus with infinitely long expressions. Colloquium mathematicum, vol. 6 (1958), pp. 165–170. - Dana Scott and Alfred Tarski. The sentential calculus with infinitely long expressions. Summaries of talks presented at the Summer Institute for Symbolic Logic, Cornell University, 1957, 2nd edn., Communications Research Division, Institute for Defense Analyses, Princeton, N.J., 1960, pp. 83–89.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 95
-
- Article
- Export citation
Alfred Tarski. Some problems and results relevant to the foundations of set theory. Logic, methodology and philosophy of science, Proceedings of the 1960 International Congress, edited by Ernest Nagel, Patrick Suppes, and Alfred Tarski, Stanford University Press, Stanford, Calif., 1962, pp. 125–135. - W. Hanf. Incompactness in languages with infinitely long expressions. Fundamenta mathematicae, vol. 53 no. 3 (1964), pp. 309–324.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 95-96
-
- Article
- Export citation
L. Henkin. Some remarks on infinitely long formulas. Infinitistic methods, Proceedings of the Symposium on Foundations of Mathematics, Warsaw, 2-9 September 1959, Państwowe Wydawnictwo Naukowe, Warsaw, and Pergamon Press, Oxford-London-New York-Paris, 1961, pp. 167–183. - Carol R. Karp. Independence proofs in predicate logic with infinitely long expressions. The journal of symbolic logic, vol. 27 no. 2 (for 1962, pub. 1963), pp. 171–188.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 96-97
-
- Article
- Export citation

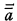 the cardinal of
the cardinal of 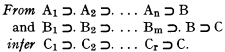
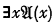 ,
, 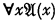 allgemeingültig ist. Die Ausdrücke, die die Identität enthalten, sind dabei eingeschlossen
allgemeingültig ist. Die Ausdrücke, die die Identität enthalten, sind dabei eingeschlossen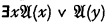 , or from this formula with any other variable in place of
, or from this formula with any other variable in place of 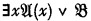 (“Upper formula” in the transitive sense of an upper formula of an upper formula being an upper formula). But then it is stated (incorrectly) that if
(“Upper formula” in the transitive sense of an upper formula of an upper formula being an upper formula). But then it is stated (incorrectly) that if 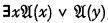 , then
, then 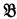 is an upper formula of
is an upper formula of 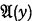 . To show that this is incorrect we here append a proof of the universally valid formula mentioned above:
. To show that this is incorrect we here append a proof of the universally valid formula mentioned above: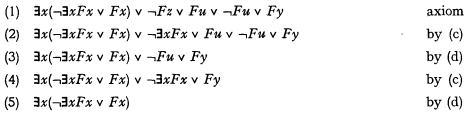
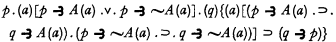
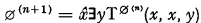 . Actually the arithmetic sets which can be expressed in prenex form with
. Actually the arithmetic sets which can be expressed in prenex form with 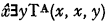 , serves to increase the “complexity” of sets in a uniform way.
, serves to increase the “complexity” of sets in a uniform way.