Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Halbeisen, Lorenz
and
Löwe, Benedikt
2001.
Techniques for approaching the dual Ramsey property in the projective hierarchy.
Pacific Journal of Mathematics,
Vol. 200,
Issue. 1,
p.
119.
Кановей, Владимир Григорьевич
Kanovei, Vladimir Grigor'evich
Любецкий, Василий Александрович
and
Lyubetskii, Vasilii Aleksandrovich
2003.
О некоторых классических проблемах дескриптивной теории множеств.
Успехи математических наук,
Vol. 58,
Issue. 5,
p.
3.
Löwe, Benedikt
2005.
The Pointwise View of Determinacy: Arboreal Forcings, Measurability, and Weak Measurability.
Rocky Mountain Journal of Mathematics,
Vol. 35,
Issue. 4,
Kysiak, Marcin
Nowik, Andrzej
and
Weiss, Tomasz
2007.
Special subsets of the reals and tree forcing notions.
Proceedings of the American Mathematical Society,
Vol. 135,
Issue. 9,
p.
2975.
Schwichtenberg, Helmut
2007.
2006 Summer Meeting of the Association for Symbolic Logic: Logic Colloquium '06.
Bulletin of Symbolic Logic,
Vol. 13,
Issue. 2,
p.
251.
Khomskii, Yurii
2008.
Logic and Its Applications.
Vol. 5378,
Issue. ,
p.
185.
Nowik, A.
and
Reardon, P.
2008.
Uniform Algebras in the Cantor and Baire Spaces.
Journal of Applied Analysis,
Vol. 14,
Issue. 2,
Ikegami, Daisuke
2009.
Projective absoluteness for Sacks forcing.
Archive for Mathematical Logic,
Vol. 48,
Issue. 7,
p.
679.
Ikegami, Daisuke
2010.
Forcing absoluteness and regularity properties.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 7,
p.
879.
BRENDLE, Jörg
and
LÖWE, Benedikt
2011.
Eventually different functions and inaccessible cardinals.
Journal of the Mathematical Society of Japan,
Vol. 63,
Issue. 1,
Brendle, Jörg
and
Khomskii, Yurii
2012.
Polarized partitions on the second level of the projective hierarchy.
Annals of Pure and Applied Logic,
Vol. 163,
Issue. 9,
p.
1345.
Halbeisen, Lorenz J.
2012.
Combinatorial Set Theory.
p.
377.
Bingham, N.H.
and
Ostaszewski, A.J.
2013.
The Steinhaus theorem and regular variation: de Bruijn and after.
Indagationes Mathematicae,
Vol. 24,
Issue. 4,
p.
679.
Laguzzi, Giorgio
2014.
Some considerations on amoeba forcing notions.
Archive for Mathematical Logic,
Vol. 53,
Issue. 5-6,
p.
487.
Laguzzi, Giorgio
2014.
On the separation of regularity properties of the reals.
Archive for Mathematical Logic,
Vol. 53,
Issue. 7-8,
p.
731.
Fischer, Vera
Friedman, Sy David
and
Khomskii, Yurii
2014.
Cichoń’s diagram, regularity properties and $${\varvec{\Delta}^1_3}$$ Δ 3 1 sets of reals.
Archive for Mathematical Logic,
Vol. 53,
Issue. 5-6,
p.
695.
Medini, Andrea
and
Zdomskyy, Lyubomyr
2015.
Between Polish and completely Baire.
Archive for Mathematical Logic,
Vol. 54,
Issue. 1-2,
p.
231.
Khomskii, Yurii
Laguzzi, Giorgio
Löwe, Benedikt
and
Sharankou, Ilya
2016.
Questions on generalised Baire spaces.
Mathematical Logic Quarterly,
Vol. 62,
Issue. 4-5,
p.
439.
Friedman, Sy David
Khomskii, Yurii
and
Kulikov, Vadim
2016.
Regularity properties on the generalized reals.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 4,
p.
408.
Halbeisen, Lorenz J.
2017.
Combinatorial Set Theory.
p.
485.
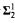 -set is measurable” and “Every
-set is measurable” and “Every  -set is measurable” for various notions of measurability derived from well-known forcing partial orderings.
-set is measurable” for various notions of measurability derived from well-known forcing partial orderings.



