Article contents
HANDMADE DENSITY SETS
Published online by Cambridge University Press: 21 March 2017
Abstract
Given a metric space (X , d), equipped with a locally finite Borel measure, a measurable set 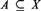 $A \subseteq X$ is a density set if the points where A has density 1 are exactly the points of A. We study the topological complexity of the density sets of the real line with Lebesgue measure, with the tools—and from the point of view—of descriptive set theory. In this context a density set is always in
$A \subseteq X$ is a density set if the points where A has density 1 are exactly the points of A. We study the topological complexity of the density sets of the real line with Lebesgue measure, with the tools—and from the point of view—of descriptive set theory. In this context a density set is always in 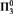 $\Pi _3^0$. We single out a family of true
$\Pi _3^0$. We single out a family of true 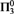 $\Pi _3^0$ density sets, an example of true
$\Pi _3^0$ density sets, an example of true 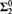 $\Sigma _2^0$ density set and finally one of true
$\Sigma _2^0$ density set and finally one of true 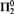 $\Pi _2^0$ density set.
$\Pi _2^0$ density set.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 1
- Cited by




