In the wake of Silver's breakthrough on the Singular Cardinals Problem (Silver [74]) followed one of the landmark results in set theory, Jensen's Covering Lemma (Devlin-Jensen [74]): If 0# does not exist then for every uncountable x ⊆ ORD there exists a constructible Y ⊇ X, card(Y) = card(X). Thus it is fair to say that in the absence of large cardinals, V is “close to L”.

It is natural to ask, as did Solovay, if we can fairly interpret the phrase “close to L” to mean “generic over L”. For example, if V = L[a], a ⊆ ω and if 0# does not exist then is V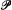-generic over L for some partial ordering 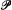∈ L? Notice that an affirmative answer implies that in the absence of 0#, no real can “code” a proper class of information.

Jensen's Coding Theorem provides a negative answer to Solovay's question, in a striking way: Any class can be “coded” by a real without introducing 0#. More precisely, if A ⊆ ORD then there is a forcing 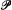definable over 〈L[A], A〉 such that 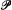⊩ V = L[a], a ⊆ ω, A is definable from a. Moreover if 0# ∉ L[A] then 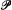⊩ 0# does not exist. Now as any M ⊨ ZFC can be generically extended to a model of the form L[A] (without introducing 0#) we obtain: For any 〈M, A〉 ⊨ ZFC (that is, M ⊨ ZFC and M obeys Replacement for formulas mentioning A as a predicate) there is an 〈M, A〉-definable forcing 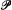such that 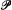⊩ V = L[a], a ⊆ ω, 〈M, A〉 is definable from a. Moreover if 0# ∉ M then 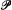⊩ 0# does not exist.