Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-01T11:27:29.068Z Has data issue: false hasContentIssue false
  • English
  • Français

DEGREE SPECTRA OF HOMEOMORPHISM TYPE OF COMPACT POLISH SPACES

Part of: Set theory Computability and recursion theory Model theory

Published online by Cambridge University Press:  11 December 2023

MATHIEU HOYRUP ,
TAKAYUKI KIHARA Open the ORCID record for TAKAYUKI KIHARA [Opens in a new window]  and
VICTOR SELIVANOV
MATHIEU HOYRUP*
Affiliation:
LORIA, UNIVERSITÉ DE LORRAINE CNRS, INRIA VILLERS-LÈS-NANCY FRANCE
TAKAYUKI KIHARA
Affiliation:
GRADUATE SCHOOL OF INFORMATICS NAGOYA UNIVERSITY NAGOYA JAPAN E-mail: kihara@i.nagoya-u.ac.jp
VICTOR SELIVANOV
Affiliation:
DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE ST. PETERSBURG STATE UNIVERSITY SAINT PETERSBURG RUSSIA and A.P. ERSHOV INSTITUTE OF INFORMATICS SYSTEMS SIBERIAN BRANCH OF THE RUSSIAN ACADEMY OF SCIENCES (SB RAS) NOVOSIBIRSK RUSSIA E-mail:vseliv@iis.nsk.su
*
E-mail: mathieu.hoyrup@inria.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

A Polish space is not always homeomorphic to a computably presented Polish space. In this article, we examine degrees of non-computability of presenting homeomorphic copies of compact Polish spaces. We show that there exists a 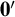$\mathbf {0}'$-computable low$_3$ compact Polish space which is not homeomorphic to a computable one, and that, for any natural number 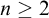$n\geq 2$, there exists a Polish space 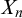$X_n$ such that exactly the high$_{n}$-degrees are required to present the homeomorphism type of 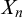$X_n$. Along the way we investigate the computable aspects of Čech homology groups. We also show that no compact Polish space has a least presentation with respect to Turing reducibility.

Keywords

computable topologycomputable presentationcomputable Polish spacedegree spectrumCech homology groups

MSC classification

Primary: 03C57: Effective and recursion-theoretic model theory 03D25: Recursively (computably) enumerable sets and degrees 03E15: Descriptive set theory
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 32
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amir, D. E. and Hoyrup, M., Strong computable type . Computability, vol. 12 (2023), no. 3, pp. 227–269.CrossRefGoogle Scholar
Ash, C. J. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy , Studies in Logic and the Foundations of Mathematics, vol. 144, North-Holland, Amsterdam, 2000.Google Scholar
Avigad, J. and Brattka, V., Computability and analysis: The legacy of Alan Turing , Turing’s Legacy: Developments from Turing’s Ideas in Logic , Lecture Notes in Logic, vol. 42, Association for Symbolic Logic, La Jolla, 2014, pp. 1–47.Google Scholar
Brattka, V. and Hertling, P., Handbook of Computability and Complexity in Analysis , Springer, Cham, 2021.CrossRefGoogle Scholar
Brattka, V., Hertling, P., and Weihrauch, K., A tutorial on computable analysis , New Computational Paradigms , Springer, New York, 2008, pp. 425–491.CrossRefGoogle Scholar
Brattka, V. and Presser, G., Computability on subsets of metric spaces . Theoretical Computer Science , vol. 305 (2003), nos. 1–3, pp. 43–76.CrossRefGoogle Scholar
Cenzer, D., ${\varPi}_1^0$ classes in computability theory, Handbook of Computability Theory , Studies in Logic and the Foundations of Mathematics, vol. 140, North-Holland, Amsterdam, 1999, pp. 37–85.CrossRefGoogle Scholar
Clanin, J., McNicholl, T. H., and Stull, D. M., Analytic computable structure theory and ${L}^p$ spaces. Fundamenta Mathematicae , vol. 244 (2019), no. 3, pp. 255–285.CrossRefGoogle Scholar
Downey, R. G. and Melnikov, A. G., Computably compact metric spaces . Bulletin of Symbolic Logic , vol. 29 (2023), no. 2, pp. 170–263.CrossRefGoogle Scholar
Eilenberg, S. and Steenrod, N., Foundations of Algebraic Topology , Princeton University Press, Princeton, 1952.CrossRefGoogle Scholar
Engelking, R., Dimension Theory , North-Holland Mathematical Studies, North-Holland, Amsterdam, 1978.Google Scholar
Ershov, Y. L., Goncharov, S. S., Nerode, A., Remmel, J. B., and Marek, V. W., editors. Handbook of Recursive Mathematics: Recursive Algebra, Analysis and Combinatorics , vol. 2 , Studies in Logic and the Foundations of Mathematics, 139, North-Holland, Amsterdam, 1998.Google Scholar
Feiner, L., Hierarchies of Boolean algebras , this Journal, vol. 35 (1970), pp. 365–374.Google Scholar
Fokina, E. B., Harizanov, V., and Melnikov, A., Computable model theory , Turing’s Legacy: Developments from Turing’s Ideas in Logic , Lecture Notes in Logic, vol. 42, Association for Symbolic Logic, La Jolla, 2014, pp. 124–194.CrossRefGoogle Scholar
Greenberg, N., Melnikov, A., Nies, A., and Turetsky, D., Effectively closed subgroups of the infinite symmetric group . Proceedings of the American Mathematical Society , vol. 146 (2018), pp. 5421–5435.CrossRefGoogle Scholar
Greenberg, N. and Montalbán, A., Ranked structures and arithmetic transfinite recursion . Transactions of the American Mathematical Society , vol. 360 (2008), no. 3, pp. 1265–1307.CrossRefGoogle Scholar
Gregoriades, V., Kispéter, T., and Pauly, A., A comparison of concepts from computable analysis and effective descriptive set theory . Mathematical Structures in Computer Science , vol. 27 (2017), no. 8, pp. 1414–1436.CrossRefGoogle Scholar
Harrison-Trainor, M., Melnikov, A., and Ng, K. M., Computability of Polish spaces up to homeomorphism , this Journal, vol. 85 (2020), no. 4, pp. 1664–1686.Google Scholar
Hatcher, A., Algebraic Topology , Cambridge University Press, Cambridge, 2002.Google Scholar
Hirschfeldt, D. R., Khoussainov, B., Shore, R. A., and Slinko, A. M., Degree spectra and computable dimensions in algebraic structures . Annals of Pure and Applied Logic , vol. 115 (2002), nos. 1–3, pp. 71–113.CrossRefGoogle Scholar
Hoyrup, M., Kihara, T., and Selivanov, V., Degree spectra of homeomorphism types of polish spaces, preprint, 2023, arXiv:2004.06872.CrossRefGoogle Scholar
Hurewicz, W. and Wallman, H., Dimension Theory (PMS-4) , Princeton University Press, Princeton, 1941.Google Scholar
Iljazovic, Z., Isometries and computability structures . Journal of Universal Computer Science , vol. 16 (2010), no. 18, pp. 2569–2596.Google Scholar
Jockusch, C. G. Jr. and Soare, Robert I., Boolean algebras, Stone spaces, and the iterated Turing jump , this Journal , vol. 59 (1994), no. 4, pp. 1121–1138.Google Scholar
Kamo, H., Effective Dini’s theorem on effectively compact metric spaces . Electronic Notes in Theoretical Computer Science , vol. 120 (2005), 73–82. Proceedings of the 6th Workshop on Computability and Complexity in Analysis (CCA 2004).CrossRefGoogle Scholar
Kechris, A. S., Classical Descriptive Set Theory , Springer, New York, 1995.CrossRefGoogle Scholar
Knight, J. F. and Stob, M., Computable Boolean algebras , this Journal, vol. 65 (2000), no. 4, pp. 1605–1623.Google Scholar
Lupini, M., Melnikov, A., and Nies, A., Computable topological abelian groups . Journal of Algebra , vol. 615 (2023), pp. 278–327.CrossRefGoogle Scholar
McNicholl, T. H. and Stull, D. M., The isometry degree of a computable copy of ${\ell}^{p1}$ . Computability , vol. 8 (2019), no. 2, pp. 179–189.CrossRefGoogle Scholar
Melnikov, A., Computable topological groups and Pontryagin duality . Transactions of the American Mathematical Society , vol. 370 (2018), 12, pp. 8709–8737.CrossRefGoogle Scholar
Melnikov, A. G., Computably isometric spaces , this Journal, vol. 78 (2013), no. 4, pp. 1055–1085.Google Scholar
Melnikov, A. G., New degree spectra of Polish spaces . Siberian Mathematical Journal , vol. 62 (2021), no. 5, pp. 882–894.CrossRefGoogle Scholar
van Mill, J., The Infinite-Dimensional Topology of Function Spaces , North-Holland Mathematical Library, vol. 64, North-Holland, Amsterdam, 2001.Google Scholar
Moschovakis, Y. N., Recursive metric spaces . Fundamenta Mathematicae , vol. 55 (1964), pp. 215–238.CrossRefGoogle Scholar
Moschovakis, Y. N., Descriptive Set Theory , second ed., Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, 2009.CrossRefGoogle Scholar
Odintsov, S. P. and Selivanov, V. L., The arithmetical hierarchy and ideals of enumerated Boolean algebras , Sibirskii Matematicheskii Zhurnal , vol. 30 (1989), no. 6, pp. 140–149.Google Scholar
Pauly, A., Seon, D., and Ziegler, M., Computing Haar measures , 28th EACSL Annual Conference on Computer Science Logic, CSL 2020, January 13–16, 2020, Barcelona, Spain (Fernández, M. and Muscholl, A., editors), Leibniz International Proceedings in Informatics, vol. 152, Schloss Dagstuhl—Leibniz-Zentrum für Informatik, Wadern, 2020, pp. 34:1–34:17.Google Scholar
Pour-El, M. B. and Ian Richards, J., Computability in Analysis and Physics , Perspectives in Mathematical Logic, Springer, Berlin, 1989.CrossRefGoogle Scholar
la Roche, P., Effective Galois theory , this Journal, vol. 46 (1981), no. 2, pp. 385–392.Google Scholar
Selivanov, V., On degree spectra of topological spaces . Lobachevskii Journal of Mathematics , vol. 41 (2020), no. 2, pp. 252–259.CrossRefGoogle Scholar
Selivanov, V. L., Algorithmic complexity of algebraic systems . Matematicheskie Zametki , vol. 44 (1988), no. 6, pp. 823–832, 863.Google Scholar
Smith, R. L., Effective aspects of profinite groups , this Journal, vol. 46 (1981), no. 4, pp. 851–863.Google Scholar
Weihrauch, K., Computable Analysis: An Introduction , Texts in Theoretical Computer Science. An EATCS Series, Springer, Berlin, 2000.CrossRefGoogle Scholar
Yasugi, M., Mori, T., and Tsujii, Y., Effective properties of sets and functions in metric spaces with computability structure . Theoretical Computer Science , vol. 219 (1999), nos. 1–2, pp. 467–486.CrossRefGoogle Scholar