Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-25T14:52:22.226Z Has data issue: false hasContentIssue false
  • English
  • Français

COUNTABLE MODELS OF THE THEORIES OF BALDWIN–SHI HYPERGRAPHS AND THEIR REGULAR TYPES

Published online by Cambridge University Press:  29 April 2019

DANUL K. GUNATILLEKA
DANUL K. GUNATILLEKA*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF MARYLAND COLLEGE PARK, MD20742, USA E-mail: danulg@math.umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We continue the study of the theories of Baldwin–Shi hypergraphs from [5]. Restricting our attention to when the rank δ is rational valued, we show that each countable model of the theory of a given Baldwin–Shi hypergraph is isomorphic to a generic structure built from some suitable subclass of the original class used in the construction. We introduce a notion of dimension for a model and show that there is a an elementary chain 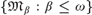$\left\{ {\mathfrak{M}_\beta :\beta \leqslant \omega } \right\}$ of countable models of the theory of a fixed Baldwin–Shi hypergraph with 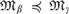$\mathfrak{M}_\beta \preccurlyeq \mathfrak{M}_\gamma $ if and only if the dimension of 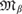$\mathfrak{M}_\beta $ is at most the dimension of 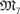$\mathfrak{M}_\gamma $ and that each countable model is isomorphic to some 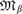$\mathfrak{M}_\beta $. We also study the regular types that appear in these theories and show that the dimension of a model is determined by a particular regular type. Further, drawing on a large body of work, we use these structures to give an example of a pseudofinite, ω-stable theory with a nonlocally modular regular type, answering a question of Pillay in [11].

Keywords

03C3003C1503C52Fraisse limitsHurshovski constructions
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 1007 - 1019
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baldwin, J. T. and Shelah, S., Randomness and semigenericity. Transactions of the AMS, vol. 349 (1997), pp. 1359–1376.Google Scholar
Baldwin, J. T. and Shelah, S., DOP and FCP in generic structures, this Journal, vol. 63 (1998), pp. 427–438.Google Scholar
Baldwin, J. T. and Shi, N., Stable generic structures. Annals of Pure and Applied Logic, vol. 79 (1996), pp. 1–35.Google Scholar
Brody, J. and Laskowski, M. C., On rational limits of Shelah-Spencer graphs , this Journal, vol. 77 (2012), pp. 580–592.Google Scholar
Gunatilleka, D. K., The theories of Baldwin-Shi hypergraphs and their atomic models, preprint, 2018, arXiv:1803.01831 [math.LO].Google Scholar
Hrushovski, E., Locally modular regular types, Classification Theory (Baldwin, J. T., editor), Springer, Berlin, Heidelberg, 1987, pp. 132–164.Google Scholar
Hrushovski, E., A new strongly minimal set. Annals of Pure and Applied Logic, vol. 62 (1993), pp. 147–166.Google Scholar
Ikeda, K., Kikyo, H., and Tsuboi, A., On generic structures with the strong amalgamation property , this Journal, vol. 74 (2009), pp. 721–733.Google Scholar
Laskowski, M. C., A simpler axiomatization of the Shelah-Spencer almost sure theories. Israel Journal of Mathematics, vol. 161 (2007), pp. 157–186.Google Scholar
Pillay, A., Geometric Stability Theory, first ed., Springer-Verlag, New York, 1996.Google Scholar
Pillay, A., Strongly minimal pseudofinite structures, preprint, 2014, arXiv:1411.5008 [math.LO].Google Scholar
Verbovskiy, V. and Yoneda, I., CM-triviality and relational structures. Annals of Pure and Applied Logic, vol. 122 (2003), pp. 175–194.Google Scholar
Wagner, F. O., Relational structures and dimensions, Automorphisms of First-Order Structures, (Kaye, R. and Macpherson, D., editors), Oxford Science Publications, Oxford University Press, New York, 1994, pp. 175–194.Google Scholar