Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-01T12:09:00.563Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPARING COMPUTABILITY IN TWO TOPOLOGIES

Part of: Computability and recursion theory Set theory Connections with other structures, applications

Published online by Cambridge University Press:  27 March 2023

DJAMEL EDDINE AMIR  and
MATHIEU HOYRUP
DJAMEL EDDINE AMIR
Affiliation:
UNIVERSITÉ DE LORRAINE CNRS, INRIA, LORIA F-54000 NANCY, FRANCE E-mail: djamel-eddine.amir@loria.fr URL: https://members.loria.fr/MHoyrup/
MATHIEU HOYRUP*
Affiliation:
UNIVERSITÉ DE LORRAINE CNRS, INRIA, LORIA F-54000 NANCY, FRANCE E-mail: djamel-eddine.amir@loria.fr URL: https://members.loria.fr/MHoyrup/
*
E-mail: mathieu.hoyrup@inria.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Computable analysis provides ways of representing points in a topological space, and therefore of defining a notion of computable points of the space. In this article, we investigate when two topologies on the same space induce different sets of computable points. We first study a purely topological version of the problem, which is to understand when two topologies are not 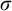$\sigma $ -homeomorphic. We obtain a characterization leading to an effective version, and we prove that two topologies satisfying this condition induce different sets of computable points. Along the way, we propose an effective version of the Baire category theorem which captures the construction technique, and enables one to build points satisfying properties that are co-meager with respect to a topology, and are computable with respect to another topology. Finally, we generalize the result to three topologies and give an application to prove that certain sets do not have computable type, which means that they have a homeomorphic copy that is semicomputable but not computable.

Keywords

Computable Polish spacecomputable pointBaire category

MSC classification

Primary: 03D78: Computation over the reals 03E15: Descriptive set theory
Secondary: 54H05: Descriptive set theory (topological aspects of Borel, analytic, projective, etc. sets)
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amir, D. E. and Hoyrup, M., Computability of finite simplicial complexes , 49th International Colloquium on Automata, Languages, and Programming (Bojanczyk, M., Merelli, E., and Woodruff, D. P., editors), LIPIcs, vol. 229, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, Wadern, 2022, pp. 111:1–111:16.Google Scholar
Amir, D. E. and Hoyrup, M., Computability of finite simplicial complexes, preprint, 2022, arXiv:2202.04945v1.CrossRefGoogle Scholar
Brattka, V., Computable versions of Baire’s category theorem , Mathematical Foundations of Computer Science 2001 (Sgall, J., Pultr, A., and Kolman, P., editors), Springer-Verlag, Berlin, 2001, pp. 224–235.CrossRefGoogle Scholar
Brattka, V., Hendtlass, M., and Kreuzer, A. P., On the uniform computational content of the Baire category theorem . Notre Dame Journal of Formal Logic , vol. 59 (2018), pp. 605–636.CrossRefGoogle Scholar
Brattka, V., Gherardi, G., and Pauly, A., Weihrauch complexity in computable analysis , Handbook of Computability and Complexity in Analysis (Brattka, V. and Hertling, P., editors), Theory and Applications of Computability, Springer, Cham, 2021, pp. 367–417.CrossRefGoogle Scholar
de Brecht, M., Quasi-Polish spaces . Annals of Pure and Applied Logic , vol. 164 (2013), no. 3, pp. 356–381.CrossRefGoogle Scholar
de Brecht, M. and Yamamoto, A., ${\varSigma}_{\alpha}^0$ -admissible representations (extended abstract) , 6th International Conference on Computability and Complexity in Analysis (Bauer, A., Hertling, P., and Ko, K.-I., editors), OpenAccess Series in Informatics (OASIcs), vol. 11, Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, Wadern, 2009.Google Scholar
Breutzmann, J. M., Juedes, D. W., and Lutz, J. H., Baire category and nowhere differentiability for feasible real functions . Mathematical Logic Quarterly , vol. 50 (2004), nos. 4–5, pp. 460–472.CrossRefGoogle Scholar
Callard, A. and Hoyrup, M., Descriptive complexity on non-polish spaces , 37th International Symposium on Theoretical Aspects of Computer Science (Paul, C. and Bläser, M., editors), LIPIcs, vol. 154, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, Wadern, 2020, pp. 8:1–8:16.Google Scholar
Debs, G., Effective decomposition of $\sigma$ -continuous Borel functions . Fundamenta Mathematicae , vol. 224 (2014), pp. 187–202.CrossRefGoogle Scholar
Hoyrup, M., Irreversible computable functions , 31st International Symposium on Theoretical Aspects of Computer Science (Mayr, E. W. and Portier, N., editors), LIPIcs, vol. 25, Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Wadern, 2014, pp. 362–373.Google Scholar
Hoyrup, M., Genericity of weakly computable objects . Theory of Computing Systems , vol. 60 (2017), no. 3, pp. 396–420.CrossRefGoogle Scholar
Iljazović, Z. and Sušić, I., Semicomputable manifolds in computable topological spaces . Journal of Complexity , vol. 45 (2018), pp. 83–114.CrossRefGoogle Scholar
Jockush, C. G., Degrees of generic sets , Recursion Theory: Its Generalisations and Applications (Drake, F. R. and Wainer, S. S., editors), Cambridge University Press, Cambridge, 1980, pp. 110–139.CrossRefGoogle Scholar
Jones, S. H., Applications of the Baire category theorem . Real Analysis Exchange , vol. 23 (1999), no. 2, pp. 363–394.CrossRefGoogle Scholar
Kalantari, I., Density & Baire category in recursive topology , Computability and Complexity in Analysis: International Conference (Brattka, V., Schröder, M., Weihrauch, K., and Zhong, N., editors), Informatik Berichte, vol. 302, FernUniversität in Hagen, Hagen, 2003, pp. 15–18.Google Scholar
Kihara, T. and Pauly, A., Point degree spectra of represented spaces . Forum of Mathematics. Sigma , vol. 10 (2022), p. e31.CrossRefGoogle Scholar
Kihara, T., Ng, K. M., and Pauly, A., Enumeration degrees and non-metrizable topology, preprint, 2020, arXiv:1904.04107.Google Scholar
Lutz, P., Results on martin’s conjecture , Ph.D. thesis, University of California, Berkeley, 2021.Google Scholar
Miller, J. S., Effectiveness for embedded spheres and balls . Electronic Notes in Theoretical Computer Science , vol. 66 (2002), no. 1, pp. 127–138.CrossRefGoogle Scholar
Pawlikowski, J. and Sabok, M., The Solecki dichotomy for bianalytic maps, preprint, 2009.Google Scholar
Pawlikowski, J. and Sabok, M., Decomposing Borel functions and structure at finite levels of the Baire hierarchy . Annals of Pure and Applied Logic , vol. 163 (2012), no. 12, pp. 1748–1764.CrossRefGoogle Scholar
Pour-El, M. B. and Richards, J. I., Computability in Analysis and Physics , Perspectives in Logic, vol. 1, Springer, Berlin, 1989.CrossRefGoogle Scholar
Schröder, M., Admissibly represented spaces and Qcb-spaces , Handbook of Computability and Complexity in Analysis (Brattka, V. and Hertling, P., editors), Springer, Cham, 2021.Google Scholar
Selivanov, V., Towards the effective descriptive set theory , Evolving Computability (Beckmann, A., Mitrana, V., and Soskova, M., editors), Springer International Publishing, Cham, 2015, pp. 324–333.CrossRefGoogle Scholar
Solecki, S., Decomposing Borel sets and functions and the structure of Baire class 1 functions . Journal of the American Mathematical Society , vol. 11 (1998), no. 3, pp. 521–550.CrossRefGoogle Scholar
Weihrauch, K., Computable Analysis , Springer, Berlin, 2000.CrossRefGoogle Scholar
Yasugi, M., Mori, T., and Tsujii, Y., Effective properties of sets and functions in metric spaces with computability structure . Theoretical Computer Science , vol. 219 (1999), nos. 1–2, pp. 467–486.CrossRefGoogle Scholar