Hostname: page-component-84b7d79bbc-lrf7s Total loading time: 0 Render date: 2024-07-29T06:35:02.970Z Has data issue: false hasContentIssue false
  • English
  • Français

On the notational independence of various hierarchies of degrees of unsolvability1

Published online by Cambridge University Press:  12 March 2014

Gustav Hensel  and
Hilary Putnam
Gustav Hensel
Affiliation:
Catholic University, Washington, D.C.
Hilary Putnam
Affiliation:
Massachusetts Institute of Technology
Get access Rights & Permissions [Opens in a new window]

Extract

From the work of Kleene, Post and Davis it is well-known that the arithmetic sets can be characterized as those sets recursive in ∅(n) for some natural number n, where ∅(0) = ∅ and 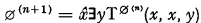. Actually the arithmetic sets which can be expressed in prenex form with n alternating quantifiers (applied to recursive predicates) are recursive in ∅(n). Hence, starting with ∅, the “jump operation”, which takes a set A into the set 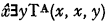, serves to increase the “complexity” of sets in a uniform way.

As far as extending the ω-sequence of degrees of unsolvability (i.e. the degrees represented by the ∅(n)) into the 2nd number class, there is an immediate problem. One knows from Spector [17], corollary 2, p. 585, that there is no l.u.b. for the ω-sequence. So, at ω one must pick a degree in some other “natural” way. Unfortunately, what has seemed “natural” to some mathematicians has not seemed natural to others. Kleene and Davis (cf. [10] and [3] respectively) extended this arithmetic hierarchy of degrees of unsolvability by making use of natural number notations for a certain segment of ordinals of the 1st and 2nd number classes, the “constructive” ordinals. Using the Church-Kleene system S3, one can “sum up” previously obtained sets at the limit notations in a way that is certainly natural from a notational point of view.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 30 , Issue 1 , March 1965 , pp. 69 - 86
Copyright
Copyright © Association for Symbolic Logic 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Added September 23, 1964. Enderton's work has now appeared: Hierarchies in recursive function theory, Transactions of the American Mathematical Society, Vol. 111 (1964), pp. 457-471.

References

BIBLIOGRAPHY

[1]Church, A., The constructive second number class, Bulletin of the American Mathematical Society, vol. 44 (1938), pp. 224–232.CrossRefGoogle Scholar
[2]Church, A. and Kleene, S. C., Formal definitions in the theory of ordinal numbers, Fundamenta Mathematicae, vol. 28 (1936), pp. 11–21.CrossRefGoogle Scholar
[3]Davis, M., On the theory of recursive unsolvability, Thesis, Princeton, 1950.Google Scholar
[4]Davis, M., Computability and Unsolvability, New York (McGraw-Hill), 1958, xxv + 210 pp.Google Scholar
[5]Hensel, G., On the notational independence of various hierarchies of degrees of unsolvability, Thesis, Princeton, 1963.Google Scholar
[6]Kleene, S. C., On notation for ordinal numbers, this Journal, vol. 3 (1938), pp. 150–155.Google Scholar
[7]Kleene, S. C., Recursive predicates and quantifiers, Transactions of the American Mathematical Society, vol. 53 (1943), pp. 41–73.CrossRefGoogle Scholar
[8]Kleene, S. C., On the forms of the predicates in the theory of constructive ordinals, American Journal of Mathematics, vol. 66 (1944), pp. 41–58.CrossRefGoogle Scholar
[9]Kleene, S. C., Introduction to Metamathematics, New York (Van Nostrand), Amsterdam (North Holland), and Groningen (Noordhoff), 1952, x + 550 pp.Google Scholar
[10]Kleene, S. C., Arithmetical predicates and function quantifiers, Transactions of the American Mathematical Society, vol. 79 (1955), pp. 312–340.CrossRefGoogle Scholar
[11]Kleene, S. C., On the forms of the predicates in the theory of constructive ordinals (second paper), American Journal of Mathematics, vol. 77 (1955), pp. 405–428.CrossRefGoogle Scholar
[12]Kleene, S. C., Hierarchies of number-theoretic predicates, Bulletin of the American Mathematical Society, vol. 61 (1955), pp. 193–213.CrossRefGoogle Scholar
[13]Kleene, S. C., Quantification of number-theoretic functions, Compositio Mathematica, vol. 14 (1959), pp. 23–40.Google Scholar
[14]Kleene, S. C. and Post, E. L., The upper semi-lattice of degrees of recursive unsolvability, Annals of Mathematics, vol. 59 (1954), pp. 379–407.CrossRefGoogle Scholar
[15]Post, E. L., Recursively enumerable sets of positive integers and their decision problems, Bulletin of the American Mathematical Society, vol. 50 (1944), pp. 284–316.CrossRefGoogle Scholar
[16]Spector, C., Recursive well-orderings, this Journal, vol. 20 (1955), pp. 151–163.Google Scholar
[17]Spector, C., On degrees of recursive unsolvability, Annals of Mathematics, vol. 64 (1956), pp. 581–592.CrossRefGoogle Scholar
[18]Spector, C., Hyperarithmetical quantifiers, Fundamenta Mathematicae, vol. 48 (1960) pp. 313–320.CrossRefGoogle Scholar