Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-24T19:33:44.383Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized cohesiveness

Published online by Cambridge University Press:  12 March 2014

Tamara Hummel  and
Carl G. Jockusch Jr.
Tamara Hummel
Affiliation:
Department of Mathematics, Allegheny College, 520 N. Main St., Meadville, PA 16335, USA E-mail: thummel@alleg.edu
Carl G. Jockusch Jr.
Affiliation:
Department of Mathematics, University of Illinois, 1409 W.Green St., Urbana, IL 61801, USA E-mail: jockusch@math.uiuc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study some generalized notions of cohesiveness which arise naturally in connection with effective versions of Ramsey's Theorem. An infinite set A of natural numbers is n-cohesive (respectively, n-r-cohesive) if A is almost homogeneous for every computably enumerable (respectively, computable) 2-coloring of the n-element sets of natural numbers. (Thus the 1-cohesive and 1-r-cohesive sets coincide with the cohesive and r-cohesive sets, respectively.) We consider the degrees of unsolvability and arithmetical definability levels of n-cohesive and n-r-cohesive sets. For example, we show that for all n ≥ 2, there exists a 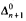n-cohesive set. We improve this result for n = 2 by showing that there is a 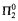2-cohesive set. We show that the n-cohesive and n-r-cohesive degrees together form a linear, non-collapsing hierarchy of degrees for n ≥ 2. In addition, for n ≥ 2 we characterize the jumps of n-cohesive degrees as exactly the degrees ≥ 0(n+1) and also characterize the jumps of the n-r-cohesive degrees.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 2 , June 1999 , pp. 489 - 516
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Cholak, P., Jockusch, C. G. Jr., and Slaman, T., On Ramsey's theorem for pairs, to appear.Google Scholar
[2] Cooper, S. B., Jump equivalence of the hyperhyperimmune sets, this Journal, vol. 37 (1972), pp. 598–600.Google Scholar
[3] Hummel, T., Effective versions of Ramsey's theorem, Ph.D. thesis , University of Illinois at Urbana–Champaign, Urbana, Illinois, 1993.Google Scholar
[4] Hummel, T., Effective versions of Ramsey's theorem: Avoiding the cone above 0′, this Journal, vol. 59 (1994), pp. 1301–1325.Google Scholar
[5] Jockusch, C. G. Jr., Ramsey's theorem and recursion theory, this Journal, vol. 37 (1972), pp. 268–280.Google Scholar
[6] Jockusch, C. G., Upward closure and cohesive degrees, Israel Journal of Mathematics, vol. 15 (1973), pp. 332–335.Google Scholar
[7] Jockusch, C. G. Jr. and Soare, R. I., classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[8] Jockusch, C. G. Jr. and Stephan, F., A cohesive set which is not high, Mathematical Logic Quarterly, vol. 39 (1993), pp. 515–530.CrossRefGoogle Scholar
[9] Jockusch, C. G., Correction to “A cohesive set which is not high”, Mathematical Logic Quarterly, vol. 43 (1997), p. 569.Google Scholar
[10] Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift fur Mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.Google Scholar
[11] Martin, D. A., Completeness, the recursion theorem, and effectively simple sets, Proceedings of the American Mathematical Society, vol. 17 (1966), pp. 838–842.Google Scholar
[12] Ramsey, F. P., On a problem informal logic, Proceedings of the London Mathematical Society, vol. 30 (1930), pp. 264–286.Google Scholar
[13] Seetapun, D. and Slaman, T., On the strength of Ramsey's theorem, Notre Dame Journal of Formal Logic, vol. 36 (1995), pp. 570–582.Google Scholar
[14] Simpson, S., Degrees ofunsolvability: a survey of results, Handbook of mathematical logic (Barwise, J., editor), North–Holland Publishing Company, Amsterdam, New York, Oxford, 1977, pp. 631–652.Google Scholar
[15] Soare, R. I., Recursively enumerable sets and degrees, Springer–Verlag, Berlin, 1987.CrossRefGoogle Scholar
[16] Soare, R. I., Computability and recursion, The Bulletin of Symbolic Logic, vol. 2 (1996), pp. 284–321.CrossRefGoogle Scholar
[17] Stephan, F., Private communication.Google Scholar