Hostname: page-component-7479d7b7d-qs9v7 Total loading time: 0 Render date: 2024-07-13T19:24:42.506Z Has data issue: false hasContentIssue false
  • English
  • Français

A functorial property of the Aczel-Buchholz-Feferman function

Published online by Cambridge University Press:  12 March 2014

Andreas Weiermann
Andreas Weiermann*
Affiliation:
Institut für Mathematische Logik und Grundlagenforschung, 48149 Münster, Germany, E-mail: weierma@math.uni-muenster.de
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Ω be the least uncountable ordinal. Let 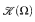be the category where the objects are the countable ordinals and where the morphisms are the strictly monotonic increasing functions. A dilator is a functor on 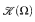which preserves direct limits and pullbacks. Let τ < ΩE ≔ min{ξ > Ω: ξ = ωξ}. Then τ has a unique “term”-representation in Ω. λξη.ωξ + η and countable ordinals called the constituents of τ. Let δ < Ω and K(τ) be the set of the constituents of τ. Let β = max K(τ). Let [β] be an occurrence of β in τ such that τ[β] = τ. Let 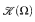be the fixed point-free version of the binary Aczel-Buchholz-Feferman-function (which is defined explicitly in the text below) which generates the Bachman-hierarchy of ordinals. It is shown by elementary calculations that 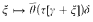is a dilator for every γ > max{β.δ.ω}.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 3 , September 1994 , pp. 945 - 955
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Buchholz, W.. Ordinal analysis of IDV, Iterated inductive definitions and subsystems of analysis: Recent proof-theoretical studies (Dold, A. and Eckmann, B., editors), Lecture Notes in Mathematics, vol. 897. Springer, Berlin, Heidelberg, New York, 1981, pp. 234–260.Google Scholar
[2]Crossley, J. N. and Kister, J. Bridge, Natural well-orderings, Archiv für Mathematische Logik und Grundlagenforschung, vol. 26 (1986/1987), pp. 57–76.Google Scholar
[3]Dershowitz, N. and Okada, M., Proof-theoretic techniques in term-rewriting theory, Proceedings of the third Annual Symposium on Logic in Computer Science, Edinburgh, Scotland, 1988, pp. 104–111.Google Scholar
[4]Feferman, S., Systems of predicative analysis II: Representations of ordinals, this Journal, vol. 33 (1968), pp. 193–220.Google Scholar
[5]Feferman, S., Proof theory: A personal report, G. Takeuti, Proof theory (Takeuti, G., editor), North-Holland, New York, Oxford, Tokyo, 1986, pp. 447–485.Google Scholar
[6]Girard, J. Y.. -logic: Part 1: Dilators, Annals of Mathematical Logic, vol. 21 (1981), pp. 75–219.CrossRefGoogle Scholar
[7]Girard, J. Y. and Vauzeilles, J., Functors and ordinal notations I: A functorial construction of the Veblen-hierarchy, this Journal, vol. 49 (1984), pp. 713–729.Google Scholar
[8]Girard, J. Y. and Vauzeilles, J.. Functors and ordinal notations II: A functorial construction of the Bachmann-hierarchy, this Journal, vol. 49 (1984), pp. 1079–1114.Google Scholar
[9]Schütte, K., Proof theory, Springer, Berlin, Heidelberg, New York, 1977.CrossRefGoogle Scholar
[10]Weiermann, A., Proving termination for term rewriting systems, Computer science logic (Börger, E., Jäger, G.. Büning, H. Kleine, and Richter, M. M.. editors), Lecture Notes in Computer Science, vol. 626, Springer, New York, 191, pp. 419–428.Google Scholar
[11]Weiermann, A., Bounds for the closure ordinals of essentially monotonic increasing functions, this Journal, vol. 58 (1993), pp. 664–671.Google Scholar
[12]Weiermann, A.. A simplified functorial construction of the Veblen-hierarchy, Mathematical Logic Quarterly, vol. 39 (1993), pp. 269–273.CrossRefGoogle Scholar