Hostname: page-component-84b7d79bbc-2l2gl Total loading time: 0 Render date: 2024-07-29T12:59:49.639Z Has data issue: false hasContentIssue false
  • English
  • Français

DEGREE OF SATISFIABILITY IN HEYTING ALGEBRAS

Part of: General logic Boolean algebras (Boolean rings) Model theory Distributive lattices

Published online by Cambridge University Press:  09 January 2024

BENJAMIN MERLIN BUMPUS Open the ORCID record for BENJAMIN MERLIN BUMPUS [Opens in a new window]  and
ZOLTAN A. KOCSIS
BENJAMIN MERLIN BUMPUS
Affiliation:
COMPUTER & INFORMATION SCIENCE & ENGINEERING UNIVERSITY OF FLORIDA GAINESVILLE FL32611, USA E-mail: benjamin.merlin.bumpus@gmail.com
ZOLTAN A. KOCSIS*
Affiliation:
SCHOOL OF COMPUTER SCIENCE AND ENGINEERING UNIVERSITY OF NEW SOUTH WALES KENSINGTON, NSW 2052, AUSTRALIA
*
E-mail: z.kocsis@unsw.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate degree of satisfiability questions in the context of Heyting algebras and intuitionistic logic. We classify all equations in one free variable with respect to finite satisfiability gap, and determine which common principles of classical logic in multiple free variables have finite satisfiability gap. In particular we prove that, in a finite non-Boolean Heyting algebra, the probability that a randomly chosen element satisfies 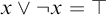$x \vee \neg x = \top $ is no larger than 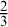$\frac {2}{3}$. Finally, we generalize our results to infinite Heyting algebras, and present their applications to point-set topology, black-box algebras, and the philosophy of logic.

Keywords

degree of satisfiabilityHeyting algebrasintuitionistic logicextremal combinatorics

MSC classification

Primary: 06D20: Heyting algebras 03B20: Subsystems of classical logic (including intuitionistic logic)
Secondary: 03C13: Finite structures
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Antolín, Y., Martino, A., and Ventura, E., Degree of commutativity of infinite groups . Proceedings of the American Mathematical Society, vol. 145 (2016), no. 2, pp. 479–485.CrossRefGoogle Scholar
Babai, L. and Szemeredi, E., On the complexity of matrix group problems I , 25th Annual Symposium on Foundations of Computer Science, Singer Island, FL, USA, 1984, pp. 229–240.CrossRefGoogle Scholar
Balbes, R. and Dwinger, P., Distributive Lattices, University of Missouri Press, Columbia, 1975.Google Scholar
Borovik, A. V. and Yalçinkaya, S., Adjoint representations of black box groups psl2(fq) . Journal of Algebra, vol. 506 (2018), pp. 540–591.CrossRefGoogle Scholar
Borovik, A. V. and Yalçinkaya, S., Homomorphic encryption and some black box attacks , Mathematical Software – ICMS 2020 (Bigatti, A. M., Carette, J., Davenport, J. H., Joswig, M., and de Wolff, T., editors), Springer, Cham, 2020, pp. 115–124.Google Scholar
Coquand, T., Spaces as distributive lattices, Mathematics: Algorithms and Proofs Workshop, 2008. http://www.cse.chalmers.se/~coquand/TRIESTE/space.pdf.Google Scholar
Delizia, C., Jezernik, U., Moravec, P., and Nicotera, C., Gaps in probabilities of satisfying some commutator-like identities . Israel Journal of Mathematics, vol. 237 (2020), no. 1, pp. 115–140.CrossRefGoogle Scholar
Glivenko, V., Sur quelques points de la logique de M. Brouwer . Bulletins de la classe des Sciences (in French), vol. 15 (1929), pp. 183–188.Google Scholar
Gustafson, W. H., What is the probability that two group elements commute? American Mathematical Monthly, vol. 80 (1973), no. 9, pp. 1031–1034.CrossRefGoogle Scholar
Hjortland, O. T., What counts as evidence for a logical theory? Australasian Journal of Logic, vol. 16 (2019), no. 7, p. 250.CrossRefGoogle Scholar
Kocsis, Z. A., Degree of satisfiability of some special equations, preprint, 2020. arXiv:2002.01773.Google Scholar
Laffey, T. J., The number of solutions of xxx=1 in a 3-group . Mathematische Zeitschrift, vol. 149 (1976), no. 1, pp. 43–45.CrossRefGoogle Scholar
Lescot, P., Isoclinism classes and commutativity degrees of finite groups . Journal of Algebra, vol. 177 (1995), no. 3, pp. 847–869.CrossRefGoogle Scholar
Pitts, A. M., On an interpretation of second order quantification in first order intuitionistic propositional logic, this Journal, vol. 57 (1992), pp. 33–521992.Google Scholar
Rieger, L., On the lattice theory of Brouwerian propositional logic, this Journal, vol. 17 (1952), no. 2, pp. 146–1471952.Google Scholar
Russell, G., The justification of the basic laws of logic . Journal of Philosophical Logic, vol. 44 (2015), no. 6, pp. 793–803.CrossRefGoogle Scholar
Williamson, T., Modal Logic as Metaphysics, Oxford University Press, Oxford, 2013.CrossRefGoogle Scholar
Yankov, V. A., On the extension of the intuitionist propositional calculus to the classical calculus, and the minimal calculus to the intuitionist calculus (in Russian) . Izvestiya Akademii Nauk SSSR Seriya Matematicheskaya, vol. 32 (1968), pp. 208–211, for an English translation, see https://iopscience.iop.org/article/10.1070/IM1968v002n01ABEH000636/pdf.Google Scholar