Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-78dcdb465f-9mfzn Total loading time: 0.24 Render date: 2021-04-19T07:22:17.765Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
The Journal of Symbolic Logic The Journal of Symbolic Logic

Article contents

Boolean algebras, Stone spaces, and the iterated Turing jump

Published online by Cambridge University Press:  12 March 2014

Carl G. Jockusch Jr.  and
Robert I. Soare
Carl G. Jockusch Jr.
Affiliation:
Department of Mathematics, University of Illinois, Urbana, Illinois 61801, E-mail: jockusch@math.uiuc.edu
Robert I. Soare
Affiliation:
Department of Mathematics, University of Chicago, Chicago, Illinois 60637, E-mail: soare@math.uchicago.edu
Corresponding
E-mail address:
jockusch@math.uiuc.edu
soare@math.uchicago.edu
Get access
Rights & Permissions[Opens in a new window]

Abstract

We show, roughly speaking, that it requires ω iterations of the Turing jump to decode nontrivial information from Boolean algebras in an isomorphism invariant fashion. More precisely, if α is a recursive ordinal, 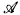is a countable structure with finite signature, and d is a degree, we say that 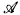has αth-jump degreed if d is the least degree which is the αth jump of some degree c such there is an isomorphic copy of 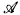with universe ω in which the functions and relations have degree at most c. We show that every degree d ≥ 0(ω) is the ωth jump degree of a Boolean algebra, but that for n < ω no Boolean algebra has nth-jump degree d < 0(n). The former result follows easily from work of L. Feiner. The proof of the latter result uses the forcing methods of J. Knight together with an analysis of various equivalences between Boolean algebras based on a study of their Stone spaces. A byproduct of the proof is a method for constructing Stone spaces with various prescribed properties.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 4 , December 1994 , pp. 1121 - 1138
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below.
If you should have access and can't see this content please contact technical support.

References

[1]Ash, C. J., Jockusch, C. G., and Knight, J. F., Jumps of orderings, Transactions of the American Mathematical Society, vol. 319 (1990), pp. 573–599.CrossRefGoogle Scholar
[2]Downey, R. and Jockusch, C. G., Every low Boolean algebra is isomorphic to a recursive one, Proceeding of the American Mathematical Society (to appear).Google Scholar
[3]Downey, R. and Knight, J. F., Orderings with αth-jump degree 0(α), Proceedings of the American Mathematical Society, vol. 114 (1992), pp. 545–552.Google Scholar
[4]Epstein, R., Degrees of unsolvability: Structure and theory, Lecture Notes in Mathematics, vol. 759, Springer-Verlag, Berlin, Heidelberg, and New York, 1979.Google Scholar
[5]Feiner, L., Hierarchies of Boolean algebras, this Journal, vol. 35 (1970), pp. 365–374.Google Scholar
[6]Jockusch, C. G. and Soare, R. I., Degrees of orderings not isomorphic to recursive linear orderings, Annals of Pure and Applied Logic, vol. 52 (1991), pp. 39–64.CrossRefGoogle Scholar
[7]Kelley, J. L., General Topology, D. Van Nostrand Company, Princeton, Toronto, New York, and London, 1955.Google Scholar
[8]Knight, J. F., Degrees coded in jumps of orderings, this Journal, vol. 51 (1986), pp. 1034–1042.Google Scholar
[9]Koppelberg, S., Boolean algebras and Boolean spaces, Handbook of Boolean algebras (Monk, J., editor), vol. 1, North-Holland, Amsterdam, New York, Oxford, and Tokyo, 1989, pp. 95–106.Google Scholar
[10]Läuchli, H., A decision procedure for the weak second order theory of linear order, Contributions to mathematical logic, Colloquium, Hannover, 1966, North-Holland, Amsterdam, 1968, pp. 189–197.Google Scholar
[11]Macintyre, J., Transfinite extensions of Friedberg's completeness criterion, this Journal, vol. 42 1977), pp. 1–10.Google Scholar
[12]Rabin, M. O., Decidability of second-order theories and automata on infinite trees, Transactions if the American Mathematical Society, vol. 141 (1969), pp. 1–35.Google Scholar
[13]Rabin, M. O., Automata on infinite objects and Church's problem, Regional Conference Series in Mathematics, Number 13, American Mathematical Society, Providence, Rhode Island, 1972.Google Scholar
[14]Remmel, J., Recursive Boolean algebras, Handbook of Boolean Algebras (Monk, J., editor), vol. 3, North-Holland, Amsterdam, New York, Oxford, and Tokyo, 1989, pp. 1097–1165.Google Scholar
[15]Richter, L. J., Degrees of unsolvability of models, Ph.D. thesis, University of Illinois Urbana-Champaign, Urbana, Illinois, 1977.Google Scholar
[16]Richter, L. J., Degrees of structures, this Journal, vol. 46 (1981), pp. 723–731.Google Scholar
[17]Rosenstein, J., Linear orderings, Academic Press, New York, 1982.Google Scholar
[18]Thurber, J., Every low2Boolean algebra has a recursive copy (to appear).Google Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 7 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 19th April 2021. This data will be updated every 24 hours.

14
Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Boolean algebras, Stone spaces, and the iterated Turing jump
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Boolean algebras, Stone spaces, and the iterated Turing jump
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Boolean algebras, Stone spaces, and the iterated Turing jump
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *