Article contents
Transient effects in the translation of bubbles insonated with acoustic pulses of finite duration
Published online by Cambridge University Press: 12 December 2017
Abstract
The translation of a bubble under the action of an acoustic forcing finds applications in fields ranging from drug delivery to sonoluminescence. This phenomenon has been widely studied for cases where the amplitude of the forcing remains constant over time. However, in many practical applications, the duration of the forcing is not long enough for the bubble to attain a constant translational velocity, mainly due to the effect of the history force. Here, we develop a formulation, valid in the limit of very viscous flow and small-amplitude acoustic forcing, that allows us to describe the transient dynamics of bubbles driven by acoustic pulses consisting of finite numbers of cycles. We also present an asymptotic solution to this theory for the case of a finite-duration sinusoidal pressure pulse. This solution takes into account both the history integral term and the transient period that the bubble needs to achieve steady radial oscillations, the former being dominant during most of the acceleration process. Moreover, by introducing some additional assumptions, we derive a simplified formula that describes the time evolution of the bubble velocity fairly well. Using this solution, we show that the convergence to the steady translational velocity, given by the so-called Bjerknes force, occurs rather slowly, namely as 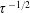 $\unicode[STIX]{x1D70F}^{-1/2}$, where
$\unicode[STIX]{x1D70F}^{-1/2}$, where  $\unicode[STIX]{x1D70F}$ is the time made dimensionless with the viscous time scale of the bubble, which explains the slow convergence of the bubble velocity and stresses the importance of taking the history force into account.
$\unicode[STIX]{x1D70F}$ is the time made dimensionless with the viscous time scale of the bubble, which explains the slow convergence of the bubble velocity and stresses the importance of taking the history force into account.
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 6
- Cited by





