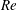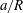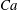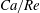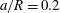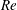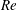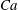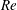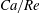1 Introduction
A capsule is a liquid droplet enclosed by a thin membrane which can resist shear deformation. Capsules are widely found in nature in the forms of red blood cells (RBCs), eggs, etc. Artificial capsules have a vast range of applications in food, cosmetic, biomedical and pharmaceutical industries (Bhujbal, de Vos & Niclou Reference Bhujbal, de Vos and Niclou2014). In many situations, capsules are suspended in a fluid and flow through a complicated network of tubes or channels: this is the case for RBCs in the human circulation or for artificial capsules flowing through microfluidic devices. Central to these flows is the dynamic motion of capsules at bifurcations, in particular the question of path selection. A good understanding of this problem is needed to elucidate some intriguing phenomena in human circulation. It will also benefit the design and optimization of microfluidic devices using branched channels, for instance to sort capsules or biological cells depending on their properties.
Extensive in vivo and in vitro experiments have been conducted on blood flows in branched capillaries or microchannels (see for instance Pries, Secomb & Gaehtgens (Reference Pries, Secomb and Gaehtgens1996) or Popel & Johnson (Reference Popel and Johnson2005)). It has been well established that the daughter branch with a higher flow rate receives a larger number of RBCs than the other branch; furthermore, one daughter branch can receive no RBC, when its flow rate is very low: this is classically referred to as the Zweifach–Fung effect (Svanes & Zweifach Reference Svanes and Zweifach1968; Fung Reference Fung1973). Similar phenomena have also been observed in experiments, where the RBCs are modelled as flexible disks and the white blood cells as solid spheres (Chien et al.
Reference Chien, Tvetenstrand, Epstein and Schmid-Schonbein1985), and in dilute suspensions of solid spheres (Roberts & Olbricht Reference Roberts and Olbricht2006; Doyeux et al.
Reference Doyeux, Podgorski, Peponas, Ismail and Coupier2011). Fenton, Carr & Cokelet (Reference Fenton, Carr and Cokelet1985) considered blood flow in a microfabricated branched tube with a diameter of 100
![]() $\unicode[STIX]{x03BC}$
m for both branches and investigated the effect of cell deformability on the partitioning of RBCs at the bifurcation. Their results, mainly the fractional RBC flux through a side branch as a function of the fractional volumetric flow rate, do not show significant differences between normal and hardened red cells. Two mechanisms have been found to play important roles in the cell enrichment in the high flow rate branch. The first one is the plasma skimming effect due to the particle-free layer near the wall of the vessel (Rong & Carr Reference Rong and Carr1990; Yan, Acrivos & Weinbaum Reference Yan, Acrivos and Weinbaum1991; Enden & Popel Reference Enden and Popel1994; Carr & Kotha Reference Carr and Kotha1995). The second mechanism is the particle screening effect, in which the trajectories of particles deviate from fluid streamlines of the background flow as a result of the hydrodynamic interaction between particles and the vessel geometry at the bifurcation (Wu, Weinbaum & Acrivos Reference Wu, Weinbaum and Acrivos1992; Doyeux et al.
Reference Doyeux, Podgorski, Peponas, Ismail and Coupier2011). In the dilute limit, the problem has not been thoroughly studied experimentally, possibly due to the difficulty of manipulating individual cells.
$\unicode[STIX]{x03BC}$
m for both branches and investigated the effect of cell deformability on the partitioning of RBCs at the bifurcation. Their results, mainly the fractional RBC flux through a side branch as a function of the fractional volumetric flow rate, do not show significant differences between normal and hardened red cells. Two mechanisms have been found to play important roles in the cell enrichment in the high flow rate branch. The first one is the plasma skimming effect due to the particle-free layer near the wall of the vessel (Rong & Carr Reference Rong and Carr1990; Yan, Acrivos & Weinbaum Reference Yan, Acrivos and Weinbaum1991; Enden & Popel Reference Enden and Popel1994; Carr & Kotha Reference Carr and Kotha1995). The second mechanism is the particle screening effect, in which the trajectories of particles deviate from fluid streamlines of the background flow as a result of the hydrodynamic interaction between particles and the vessel geometry at the bifurcation (Wu, Weinbaum & Acrivos Reference Wu, Weinbaum and Acrivos1992; Doyeux et al.
Reference Doyeux, Podgorski, Peponas, Ismail and Coupier2011). In the dilute limit, the problem has not been thoroughly studied experimentally, possibly due to the difficulty of manipulating individual cells.
Analysing the motion of one capsule flowing through a branched tube theoretically or numerically is also very challenging due to the strong nonlinear interactions between the elastic capsule, the viscous fluid and the branched geometry of the tube. The problem has mostly been studied in recent years using two-dimensional numerical models. Secomb, Styp-Rekowska & Pries (Reference Secomb, Styp-Rekowska and Pries2007) pioneered the simulation of flows with capsules through a bifurcation with a finite element model. Using a two-dimensional formulation, they predicted the trajectories of RBCs in branched microvessels of the rat mesentery, which are in qualitative agreement with experimental observations. Later, the same group found that the cell enrichment in the higher flow rate branch is increased by the cell deformability (Barber et al. Reference Barber, Alberding, Restrepo and Secomb2008). Recently they studied the effect of cell interaction and found that it leads to a more uniform cell partitioning compared with dilute suspensions, in which cell interaction is negligible (Barber, Restrepo & Secomb Reference Barber, Restrepo and Secomb2011). Woolfenden & Blyth (Reference Woolfenden and Blyth2011) developed a two-dimensional boundary integral method and studied the motion and deformation of a capsule in a channel with a side branch. The capsule was released along the centreline of the parent channel. Their results showed that, at equal flow rate between the two downstream channels, the capsule tends to flow into the side branch in particular when the capsule is highly deformable.
To the best of our knowledge, there is so far no systematic and in-depth three-dimensional numerical study of a deformable capsule in a branched tube. To what extent the results obtained from previous two-dimensional simulations can be applied to three-dimensional flows remains unclear. Almost all the previous studies have considered two-dimensional situations under low Reynolds number conditions. The negligible inertia condition is a good assumption in many biological systems; however, capsules are not necessarily small in size, and the flow speed can be fast in some applications, such as in the case of inertial flow focusing of spherical and anisotropic particles (Di Carlo et al. Reference Di Carlo, Irimia, Tompkins and Toner2007; Masaeli et al. Reference Masaeli, Sollier, Amini, Mao, Camacho, Doshi, Mitragotri, Alexeev and Di Carlo2012). The effect of inertia on path selection of a capsule at a bifurcation remains unknown. In other systems, for example non-spherical particles in shear flows, it has been shown that inertial effect could fundamentally change the dynamics of particles even at low Reynolds number (Rosén, Lundell & Aidun Reference Rosén, Lundell and Aidun2014; Dabade, Marath & Subramanian Reference Dabade, Marath and Subramanian2016). Furthermore, when a capsule approaches the bifurcation, it can sustain high shear stresses, which may damage the capsule membrane. It is therefore meaningful to investigate the membrane tension of the capsule at the bifurcation. In the present study, we address these open questions by means of computational simulations based on an immersed-boundary lattice Boltzmann method.
The paper is organized as follows: the problem, governing equations and main parameters are detailed in § 2; the numerical method and validations are then presented in § 3. We first present simulation results of flows in a branched tube without a capsule in § 4. The results for flows with a capsule are presented in § 5, where we focus on the effects of flow split ratio, flow strength and capsule properties (i.e. membrane shear elasticity, capsule size) on the capsule path selection. In § 6, we discuss the main results and compare them to the predictions of a simplified model of the capsule path selection. We also assess the experimental feasibility of the device and discuss its potential for capsules sorting.
2 Problem statement
2.1 Problem description
We consider the flow of an initially spherical capsule in a cylindrical tube with a right-angled cylindrical side branch, which has the same diameter
![]() $2R$
(figure 1
a). The length of the parent tube is
$2R$
(figure 1
a). The length of the parent tube is
![]() $12R$
, and the length of the two daughter tubes is
$12R$
, and the length of the two daughter tubes is
![]() $10R$
. A three-dimensional Cartesian coordinate system is defined with the
$10R$
. A three-dimensional Cartesian coordinate system is defined with the
![]() $x$
-axis along the straight tube axis, the
$x$
-axis along the straight tube axis, the
![]() $z$
-axis along the side branch axis and
$z$
-axis along the side branch axis and
![]() $x=y=z=0$
at the bifurcation centre. The capsule is initially spherical with diameter
$x=y=z=0$
at the bifurcation centre. The capsule is initially spherical with diameter
![]() $2a$
. It is enclosed by a hyperelastic membrane with finite surface shear elasticity and bending stiffness. The fluids inside and outside the capsule have identical viscosity
$2a$
. It is enclosed by a hyperelastic membrane with finite surface shear elasticity and bending stiffness. The fluids inside and outside the capsule have identical viscosity
![]() $\unicode[STIX]{x1D707}$
and density
$\unicode[STIX]{x1D707}$
and density
![]() $\unicode[STIX]{x1D70C}$
. Numerical simulations of capsules in a straight tube (Helmy & Barthès-Biesel Reference Helmy and Barthès-Biesel1982; Pozrikidis Reference Pozrikidis2005a
,Reference Pozrikidis
b
) have shown that the capsule migrates to the centreline of the tube and eventually reaches a steady shape. In the present study, the capsule centre is thus initially positioned on the centreline of the parent tube within the cross-section
$\unicode[STIX]{x1D70C}$
. Numerical simulations of capsules in a straight tube (Helmy & Barthès-Biesel Reference Helmy and Barthès-Biesel1982; Pozrikidis Reference Pozrikidis2005a
,Reference Pozrikidis
b
) have shown that the capsule migrates to the centreline of the tube and eventually reaches a steady shape. In the present study, the capsule centre is thus initially positioned on the centreline of the parent tube within the cross-section
![]() $S_{c}$
, located at a distance
$S_{c}$
, located at a distance
![]() $2R$
from the tube entrance
$2R$
from the tube entrance
![]() $S_{0}$
(figure 1
a).
$S_{0}$
(figure 1
a).

Figure 1. (a) Geometry of the branched tube. (b) Geometry of the computational domain.
The fluid motion in the branched tube is governed by the Navier–Stokes equations, which are solved by means of a lattice Boltzmann method (LBM) as detailed in § 3.1. At the tube wall a no-slip boundary condition is imposed. At the upstream inlet
![]() $S_{0}$
and the two downstream outlets
$S_{0}$
and the two downstream outlets
![]() $S_{1}$
and
$S_{1}$
and
![]() $S_{2}$
, the velocity profiles are set to be the parabolic Poiseuille profiles corresponding to flow rates
$S_{2}$
, the velocity profiles are set to be the parabolic Poiseuille profiles corresponding to flow rates
![]() $Q_{0}$
,
$Q_{0}$
,
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
, respectively, with
$Q_{2}$
, respectively, with
![]() $Q_{0}=Q_{1}+Q_{2}$
. The present set-up is relevant to microfluidic applications where the flow rate is controlled by multiple syringe pumps.
$Q_{0}=Q_{1}+Q_{2}$
. The present set-up is relevant to microfluidic applications where the flow rate is controlled by multiple syringe pumps.
The thickness of the capsule wall is assumed to be infinitely small. A very thin hyperelastic membrane can be modelled as a zero-thickness elastic surface, with different possible constitutive laws (Barthès-Biesel Reference Barthès-Biesel2016). Among those, the Skalak’s (SK) law (Skalak et al. Reference Skalak, Tozeren, Zarda and Chien1973), which was originally proposed to describe the membrane of a RBC, assumes a strain energy function of the form
where
![]() $W$
is the strain energy density per unit undeformed surface area,
$W$
is the strain energy density per unit undeformed surface area,
![]() $G_{s}$
is the surface shear elasticity modulus,
$G_{s}$
is the surface shear elasticity modulus,
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
are the first and second strain invariants of the surface deformation with
$I_{2}$
are the first and second strain invariants of the surface deformation with
![]() $I_{1}={\unicode[STIX]{x1D706}_{1}}^{2}+{\unicode[STIX]{x1D706}_{2}}^{2}-2$
and
$I_{1}={\unicode[STIX]{x1D706}_{1}}^{2}+{\unicode[STIX]{x1D706}_{2}}^{2}-2$
and
![]() $I_{2}=(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2})^{2}-1=(\text{d}A/\text{d}A_{0})^{2}-1$
. Here
$I_{2}=(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2})^{2}-1=(\text{d}A/\text{d}A_{0})^{2}-1$
. Here
![]() $\text{d}A_{0}$
and
$\text{d}A_{0}$
and
![]() $\text{d}A$
are the initial and final infinitesimal areas of a membrane element. The terms
$\text{d}A$
are the initial and final infinitesimal areas of a membrane element. The terms
![]() $\unicode[STIX]{x1D706}_{1}$
and
$\unicode[STIX]{x1D706}_{1}$
and
![]() $\unicode[STIX]{x1D706}_{2}$
are the principal extension ratios in the plane of the membrane (square root of the eigenvalues of the Cauchy–Green surface deformation tensor). Postulated in such a way, the SK law captures the special feature of biological membranes, which can deform easily under shear while keeping an almost constant surface area. The factor
$\unicode[STIX]{x1D706}_{2}$
are the principal extension ratios in the plane of the membrane (square root of the eigenvalues of the Cauchy–Green surface deformation tensor). Postulated in such a way, the SK law captures the special feature of biological membranes, which can deform easily under shear while keeping an almost constant surface area. The factor
![]() $C$
on the right-hand side of (2.1) must be large to ensure negligible area dilation. The principal membrane tensions
$C$
on the right-hand side of (2.1) must be large to ensure negligible area dilation. The principal membrane tensions
![]() $\unicode[STIX]{x1D70F}_{1}$
and
$\unicode[STIX]{x1D70F}_{1}$
and
![]() $\unicode[STIX]{x1D70F}_{2}$
in the membrane plane are given by
$\unicode[STIX]{x1D70F}_{2}$
in the membrane plane are given by
Another constitutive law is the two-dimensional neo–Hookean (NH) law (Green & Adkins Reference Green and Adkins1960), which assumes that the membrane is an infinitely thin sheet of a three-dimensional isotropic volume-incompressible material. The membrane area dilation is compensated by membrane thinning, since the principal extension ratio in the direction perpendicular to the membrane is equal to
![]() $\unicode[STIX]{x1D706}_{3}=1/\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}$
. The strain energy function of the NH law is given by
$\unicode[STIX]{x1D706}_{3}=1/\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}$
. The strain energy function of the NH law is given by
so that the principal elastic tensions read
The SK law leads to the same small deformation behaviour as the NH law when
![]() $C=1$
(Barthès-Biesel, Diaz & Dhenin Reference Barthès-Biesel, Diaz and Dhenin2002). For biological membranes, the factor
$C=1$
(Barthès-Biesel, Diaz & Dhenin Reference Barthès-Biesel, Diaz and Dhenin2002). For biological membranes, the factor
![]() $C$
is usually much larger than unity, because of their quasi area incompressibility. In the case of artificial capsules, the SK law has been found to fit experimental data when values of order
$C$
is usually much larger than unity, because of their quasi area incompressibility. In the case of artificial capsules, the SK law has been found to fit experimental data when values of order
![]() $1$
are used for the factor
$1$
are used for the factor
![]() $C$
(Carin et al.
Reference Carin, Barthès-Biesel, Edwards-Lévy, Postel and Andrei2003; Risso & Carin Reference Risso and Carin2004; Rachik et al.
Reference Rachik, Barthès-Biesel, Carin and Edwards-Lévy2006). In the present study, the simulations are conducted for capsules enclosed by an SK membrane with
$C$
(Carin et al.
Reference Carin, Barthès-Biesel, Edwards-Lévy, Postel and Andrei2003; Risso & Carin Reference Risso and Carin2004; Rachik et al.
Reference Rachik, Barthès-Biesel, Carin and Edwards-Lévy2006). In the present study, the simulations are conducted for capsules enclosed by an SK membrane with
![]() $C=1$
, unless otherwise stated.
$C=1$
, unless otherwise stated.
The bending resistance of the membrane is modelled using Helfrich’s formulation (Zhong-Can & Helfrich Reference Zhong-Can and Helfrich1989; Cordasco & Bagchi Reference Cordasco and Bagchi2013)
In this equation
![]() $E_{b}$
is the bending energy of the capsule membrane,
$E_{b}$
is the bending energy of the capsule membrane,
![]() $A$
the surface area,
$A$
the surface area,
![]() $k_{c}$
the bending rigidity,
$k_{c}$
the bending rigidity,
![]() $H$
the mean curvature and
$H$
the mean curvature and
![]() $c_{0}$
the spontaneous curvature corresponding to the natural state of the unstressed membrane. For the present spherical capsules
$c_{0}$
the spontaneous curvature corresponding to the natural state of the unstressed membrane. For the present spherical capsules
![]() $c_{0}=0$
has been used.
$c_{0}=0$
has been used.
The interaction between the fluid and capsule membrane is solved by an immersed-boundary method (IBM), which is described in § 3.1.
2.2 Main parameters
The problem depends on a number of dimensionless parameters, which pertain to the flow configuration and to the capsule properties.
-
(i) The branch flow ratio
 $q$
is the flow rate in the side branch normalized by the flow rate in the parent tube: (2.6)where
$q$
is the flow rate in the side branch normalized by the flow rate in the parent tube: (2.6)where $$\begin{eqnarray}q=\frac{Q_{2}}{Q_{1}+Q_{2}},\end{eqnarray}$$
$$\begin{eqnarray}q=\frac{Q_{2}}{Q_{1}+Q_{2}},\end{eqnarray}$$
 $Q_{1}$
and
$Q_{1}$
and
 $Q_{2}$
are the flow rates in the downstream main tube and in the side branch, respectively, as indicated in figure 1(a).
$Q_{2}$
are the flow rates in the downstream main tube and in the side branch, respectively, as indicated in figure 1(a).
-
(ii) The flow Reynolds number
 $Re$
is evaluated in the parent tube: (2.7)where
$Re$
is evaluated in the parent tube: (2.7)where $$\begin{eqnarray}Re=\frac{2\unicode[STIX]{x1D70C}VR}{\unicode[STIX]{x1D707}},\end{eqnarray}$$
$$\begin{eqnarray}Re=\frac{2\unicode[STIX]{x1D70C}VR}{\unicode[STIX]{x1D707}},\end{eqnarray}$$
 $V$
is the mean velocity of the Poiseuille flow imposed at the inlet of the parent tube.
$V$
is the mean velocity of the Poiseuille flow imposed at the inlet of the parent tube.
-
(iii) The size ratio
 $a/R$
compares the size of the capsule to that of the tube.
$a/R$
compares the size of the capsule to that of the tube. -
(iv) The capillary number or dimensionless shear rate
 $Ca$
measures the ratio between the viscous and elastic forces in the parent tube: (2.8)
$Ca$
measures the ratio between the viscous and elastic forces in the parent tube: (2.8) $$\begin{eqnarray}Ca=\frac{\unicode[STIX]{x1D707}V}{G_{s}}.\end{eqnarray}$$
$$\begin{eqnarray}Ca=\frac{\unicode[STIX]{x1D707}V}{G_{s}}.\end{eqnarray}$$
-
(v) The dimensionless bending stiffness
 $B$
measures the relative importance of the membrane bending to shear elastic effects: (2.9)Unless otherwise specified, a small value of
$B$
measures the relative importance of the membrane bending to shear elastic effects: (2.9)Unless otherwise specified, a small value of $$\begin{eqnarray}B=\frac{k_{c}}{G_{s}R^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}B=\frac{k_{c}}{G_{s}R^{2}}.\end{eqnarray}$$
 $B$
has been used (
$B$
has been used (
 $B=0.0008$
) mainly to prevent the formation of membrane wrinkles (Dupont et al.
Reference Dupont, Salsac, Barthès-Biesel, Vidrascu and Le Tallec2015).
$B=0.0008$
) mainly to prevent the formation of membrane wrinkles (Dupont et al.
Reference Dupont, Salsac, Barthès-Biesel, Vidrascu and Le Tallec2015).
Equations (2.7) and (2.8) clearly show that the capillary number and the Reynolds number both increase with
![]() $V$
and are related by
$V$
and are related by
Their ratio depends only on the physical properties of the tube flow and of the capsule.
3 Numerical method and validation
3.1 Numerical method
The present simulations are based on a lattice Boltzmann method (LBM) to compute the flow coupled with the immersed-boundary method (IBM) of Peskin (Reference Peskin1977) for the fluid–capsule interaction. A finite element method is used to obtain the membrane forces. This hybrid method has been validated extensively against results of boundary element simulations and of a small deformation theory for three-dimensional capsules in shear flow (Sui et al. Reference Sui, Chew, Roy and Low2008a ,Reference Sui, Low, Chew and Roy b ). The method is only briefly presented here, but more details can be found in the cited references.
The LBM is a kinetic-based approach for simulating fluid flows. Instead of solving the conservation equation of macroscopic properties such as mass or momentum, it consists in modelling the fluid as fictive particles that propagate and collide on a discrete lattice mesh. Solving for the streaming and collision steps lead to solving the following equation (Guo, Zheng & Shi Reference Guo, Zheng and Shi2002a ):
where
![]() $f_{i}(\boldsymbol{x},t)$
is the distribution function for particles with velocity
$f_{i}(\boldsymbol{x},t)$
is the distribution function for particles with velocity
![]() $\boldsymbol{e}_{i}$
at position
$\boldsymbol{e}_{i}$
at position
![]() $\boldsymbol{x}$
and time
$\boldsymbol{x}$
and time
![]() $t$
,
$t$
,
![]() $\unicode[STIX]{x0394}t$
is the lattice time interval,
$\unicode[STIX]{x0394}t$
is the lattice time interval,
![]() $f_{i}^{eq}(\boldsymbol{x},t)$
is the equilibrium distribution function,
$f_{i}^{eq}(\boldsymbol{x},t)$
is the equilibrium distribution function,
![]() $\unicode[STIX]{x1D70F}$
is the non-dimensional relaxation time related to the fluid viscosity and
$\unicode[STIX]{x1D70F}$
is the non-dimensional relaxation time related to the fluid viscosity and
![]() $F_{i}$
is the forcing term. The macroscopic quantities (e.g. velocity, pressure) can be obtained from the particle distribution function. Equation (3.1) is solved on a uniform Cartesian grid in a domain
$F_{i}$
is the forcing term. The macroscopic quantities (e.g. velocity, pressure) can be obtained from the particle distribution function. Equation (3.1) is solved on a uniform Cartesian grid in a domain
![]() $24R\times 2R\times 12R$
(figure 1
b). Using Chapman–Enskog expansion, the lattice Boltzmann equation can recover the incompressible Navier–Stokes equations, and therefore the LBM can be considered as an alternative approach for solving the Navier–Stokes equations.
$24R\times 2R\times 12R$
(figure 1
b). Using Chapman–Enskog expansion, the lattice Boltzmann equation can recover the incompressible Navier–Stokes equations, and therefore the LBM can be considered as an alternative approach for solving the Navier–Stokes equations.
To handle the curved solid wall of the branched tube, we have used the second-order bounce-back scheme developed by Bouzidi, Firdaouss & Lallemand (Reference Bouzidi, Firdaouss and Lallemand2001), which is an accurate and simple treatment. The bounce-back scheme mimics the particle–boundary interaction for no-slip boundary condition by reversing the momentum of the particle colliding with an impenetrable and rigid wall. In the approach of Bouzidi et al. (Reference Bouzidi, Firdaouss and Lallemand2001), the tube wall can be off the grid points of the regular computational domain (shown in figure 1 b for the present case), which is covered by regular Cartesian mesh. Due to the presence of the wall, the particle distribution functions at the fluid nodes nearest to the wall are unknown in some directions after the streaming step in the LBM: they are reconstructed by a second-order interpolation. The approach has been widely used in treating no-slip walls with complicated geometries. More details can be found in the paper by Bouzidi et al. (Reference Bouzidi, Firdaouss and Lallemand2001) and are not repeated here. At the inlet and outlets of the tube, velocity boundary conditions assuming fully developed Poiseuille flows with the appropriate flow rates have been implemented using a second-order non-equilibrium extrapolation method (Guo, Zheng & Shi Reference Guo, Zheng and Shi2002b ).
In the IBM, a force density is distributed on the Cartesian mesh in the vicinity of the moving boundary in order to account for the presence of the solid boundary. Two different coordinate systems are used: the fluid region is represented by Eulerian coordinates and the membrane of the moving capsule immersed in the fluid by Lagrangian ones. Across the capsule membrane the fluid velocity is continuous and the no-slip boundary condition is satisfied by letting the flexible membrane move at the same velocity as the fluid around it. This motion causes the capsule to deform. There is a jump in fluid stress across the capsule membrane, which is balanced by the membrane stress, calculated from the constitutive laws of the elastic membrane (2.1), (2.3) or (2.5). The membrane force at a Lagrangian mesh point is distributed on the Eulerian fluid grid points near it by a three-dimensional Dirac delta function. It is commonly accepted that the procedure is efficient if the mesh size ratio between the Lagrangian and Eulerian grids is less than unity. More details can be found in Sui et al. (Reference Sui, Chew, Roy and Low2008a ).
In the present study, the three-dimensional capsule membrane is discretized into flat triangular elements, following the approach of Ramanujan & Pozrikidis (Reference Ramanujan and Pozrikidis1998). To discretize the unstressed spherical capsule wall, each triangular face of a regular octahedron is subdivided into
![]() $4^{n}$
triangular elements. These elements are then projected radially onto the sphere. Note that for a given number of elements, the membrane mesh size depends on the capsule radius. In order to obtain the membrane force due to deformation, a finite element model developed by Charrier, Shrivastava & Wu (Reference Charrier, Shrivastava and Wu1989) and Shrivastava & Tang (Reference Shrivastava and Tang1993) has been employed.
$4^{n}$
triangular elements. These elements are then projected radially onto the sphere. Note that for a given number of elements, the membrane mesh size depends on the capsule radius. In order to obtain the membrane force due to deformation, a finite element model developed by Charrier, Shrivastava & Wu (Reference Charrier, Shrivastava and Wu1989) and Shrivastava & Tang (Reference Shrivastava and Tang1993) has been employed.
3.2 Validation
We first validate the model for tube flows by considering a large spherical capsule (
![]() $a/R=0.9$
) flowing in a long straight tube (length
$a/R=0.9$
) flowing in a long straight tube (length
![]() $20R$
). A grid size of
$20R$
). A grid size of
![]() $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=\unicode[STIX]{x0394}z=0.04R$
has been used for the fluid domain. The three-dimensional capsule membrane is discretized into 32 768 flat triangular elements connecting 16 386 nodes, leading to a maximum element edge length
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=\unicode[STIX]{x0394}z=0.04R$
has been used for the fluid domain. The three-dimensional capsule membrane is discretized into 32 768 flat triangular elements connecting 16 386 nodes, leading to a maximum element edge length
![]() $\unicode[STIX]{x0394}L_{c}\sim 0.034R$
and a ratio
$\unicode[STIX]{x0394}L_{c}\sim 0.034R$
and a ratio
![]() $\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x<0.86$
. We obtain the capsule profiles at equilibrium and compare them with those obtained by Hu, Salsac & Barthès-Biesel (Reference Hu, Salsac and Barthès-Biesel2012) who used a boundary element method. Very good agreement was achieved in all the cases that were tested. As an illustration, figure 2 shows the superposition of the deformed profiles obtained with both methods for a capsule with a NH membrane and a size ratio of
$\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x<0.86$
. We obtain the capsule profiles at equilibrium and compare them with those obtained by Hu, Salsac & Barthès-Biesel (Reference Hu, Salsac and Barthès-Biesel2012) who used a boundary element method. Very good agreement was achieved in all the cases that were tested. As an illustration, figure 2 shows the superposition of the deformed profiles obtained with both methods for a capsule with a NH membrane and a size ratio of
![]() $a/R=0.9$
under different capillary numbers. We also conducted simulations with a coarser membrane mesh (8192 flat triangular elements connecting 4098 nodes) and found that for
$a/R=0.9$
under different capillary numbers. We also conducted simulations with a coarser membrane mesh (8192 flat triangular elements connecting 4098 nodes) and found that for
![]() $Ca=0.1$
the deformed profiles were superimposed within graphical precision.
$Ca=0.1$
the deformed profiles were superimposed within graphical precision.

Figure 2. Steady profiles of an initially spherical capsule with a NH membrane in a uniform tube flow (
![]() $a/R=0.9$
,
$a/R=0.9$
,
![]() $Re=0.125$
,
$Re=0.125$
,
![]() $B=0$
) for
$B=0$
) for
![]() $Ca=0.02$
, 0.05, 0.1 (from left to right). Black solid lines correspond to the present model with a membrane mesh of 32 768 flat triangular elements connecting 16 386 nodes. The results are compared to the ones obtained by Hu et al. (Reference Hu, Salsac and Barthès-Biesel2012) using a boundary element method (square symbols).
$Ca=0.02$
, 0.05, 0.1 (from left to right). Black solid lines correspond to the present model with a membrane mesh of 32 768 flat triangular elements connecting 16 386 nodes. The results are compared to the ones obtained by Hu et al. (Reference Hu, Salsac and Barthès-Biesel2012) using a boundary element method (square symbols).
We now turn to the flow of a capsule in the bifurcation and investigate first the influence of the mesh size of the uniform Cartesian grid that is used in the flow domain (figure 1
b). We consider a small capsule (
![]() $a/R=0.4$
) with a membrane mesh of 8192 flat triangular elements connecting 4098 nodes, leading to
$a/R=0.4$
) with a membrane mesh of 8192 flat triangular elements connecting 4098 nodes, leading to
![]() $\unicode[STIX]{x0394}L_{c}\sim 0.031R$
. Figure 3 shows an example of the influence of the flow grid resolution on the trajectories the capsule in the branched tube for
$\unicode[STIX]{x0394}L_{c}\sim 0.031R$
. Figure 3 shows an example of the influence of the flow grid resolution on the trajectories the capsule in the branched tube for
![]() $Re=0.25$
,
$Re=0.25$
,
![]() $Ca=0.5$
and
$Ca=0.5$
and
![]() $q=0.5$
. We find that the trajectories are almost superimposed for all three tested flow grids (
$q=0.5$
. We find that the trajectories are almost superimposed for all three tested flow grids (
![]() $\unicode[STIX]{x0394}x=0.05R,0.04R$
and
$\unicode[STIX]{x0394}x=0.05R,0.04R$
and
![]() $0.031R$
). Further refining the membrane mesh to 32 768 flat triangular elements connecting 16 386 nodes (
$0.031R$
). Further refining the membrane mesh to 32 768 flat triangular elements connecting 16 386 nodes (
![]() $\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x<0.38$
for
$\unicode[STIX]{x0394}L_{c}/\unicode[STIX]{x0394}x<0.38$
for
![]() $\unicode[STIX]{x0394}x=0.04R$
) does not lead to any visible change in the capsule trajectory. The fluid mesh was chosen, so that the fluid film between the capsule wall and the tube was resolved by at least three grid spaces. Figure 3 illustrates one instance, where the capsule gets very close to the tube wall, as it enters the side branch. We have found that the grid size of
$\unicode[STIX]{x0394}x=0.04R$
) does not lead to any visible change in the capsule trajectory. The fluid mesh was chosen, so that the fluid film between the capsule wall and the tube was resolved by at least three grid spaces. Figure 3 illustrates one instance, where the capsule gets very close to the tube wall, as it enters the side branch. We have found that the grid size of
![]() $\unicode[STIX]{x0394}x=0.04R$
guarantees, even in this case, that the fluid film contains more than three grid spaces. All the results presented hereafter have thus been obtained for a capsule mesh made of 8192 flat triangular elements connecting 4098 nodes and for a fluid grid
$\unicode[STIX]{x0394}x=0.04R$
guarantees, even in this case, that the fluid film contains more than three grid spaces. All the results presented hereafter have thus been obtained for a capsule mesh made of 8192 flat triangular elements connecting 4098 nodes and for a fluid grid
![]() $\unicode[STIX]{x0394}x=0.04R$
.
$\unicode[STIX]{x0394}x=0.04R$
.

Figure 3. Trajectories of a capsule (
![]() $a/R=0.4$
) flowing in the branched tube at
$a/R=0.4$
) flowing in the branched tube at
![]() $Re=0.25,Ca=0.5,q=0.5$
. Different grid resolutions are used:
$Re=0.25,Ca=0.5,q=0.5$
. Different grid resolutions are used:
![]() $\unicode[STIX]{x0394}x=0.05R$
(dash-dot line),
$\unicode[STIX]{x0394}x=0.05R$
(dash-dot line),
![]() $\unicode[STIX]{x0394}x=0.04R$
(solid line),
$\unicode[STIX]{x0394}x=0.04R$
(solid line),
![]() $\unicode[STIX]{x0394}x=0.031R$
(dash line).
$\unicode[STIX]{x0394}x=0.031R$
(dash line).
The effect of the length of the tubes has also been studied. After being released, the capsule deforms into a steady shape, once its centre of mass has travelled a distance of approximately
![]() $5R$
from its initial position in
$5R$
from its initial position in
![]() $S_{c}$
. The
$S_{c}$
. The
![]() $12R$
length of the parent tube is, therefore, long enough for the capsule to reach an equilibrium profile before the bifurcation. We have also examined the effect of the lengths of both downstream tubes by extending them to
$12R$
length of the parent tube is, therefore, long enough for the capsule to reach an equilibrium profile before the bifurcation. We have also examined the effect of the lengths of both downstream tubes by extending them to
![]() $14R$
, and found almost identical trajectories of the capsule at the bifurcation. Thus the downstream tubes are long enough to exclude the effect of the downstream boundaries on the capsule motion at the bifurcation. However, it should be noted that the capsule does not reach a steady shape in any downstream branch after passing the bifurcation. Although distance of about
$14R$
, and found almost identical trajectories of the capsule at the bifurcation. Thus the downstream tubes are long enough to exclude the effect of the downstream boundaries on the capsule motion at the bifurcation. However, it should be noted that the capsule does not reach a steady shape in any downstream branch after passing the bifurcation. Although distance of about
![]() $5R$
after the bifurcation is sufficient for the background flow in each branch (i.e. without a capsule) to relax into the fully developed Poiseuille flow at
$5R$
after the bifurcation is sufficient for the background flow in each branch (i.e. without a capsule) to relax into the fully developed Poiseuille flow at
![]() $Re\leqslant 40$
, much longer distances are required for the capsule to regain its steady-state shape downstream of the bifurcation. It indeed relies on the capsule migration back towards the tube centreline, which is a very long process (Helmy & Barthès-Biesel Reference Helmy and Barthès-Biesel1982; Pozrikidis Reference Pozrikidis2005b
; Doddi & Bagchi Reference Doddi and Bagchi2008). As pointed out by Woolfenden & Blyth (Reference Woolfenden and Blyth2011) and Ye, Huang & Lu (Reference Ye, Huang and Lu2015), a much longer downstream tube (typically tens of the diameter of the tube) is needed for the capsule to relax into a steady state, which is beyond the scope of the present study.
$Re\leqslant 40$
, much longer distances are required for the capsule to regain its steady-state shape downstream of the bifurcation. It indeed relies on the capsule migration back towards the tube centreline, which is a very long process (Helmy & Barthès-Biesel Reference Helmy and Barthès-Biesel1982; Pozrikidis Reference Pozrikidis2005b
; Doddi & Bagchi Reference Doddi and Bagchi2008). As pointed out by Woolfenden & Blyth (Reference Woolfenden and Blyth2011) and Ye, Huang & Lu (Reference Ye, Huang and Lu2015), a much longer downstream tube (typically tens of the diameter of the tube) is needed for the capsule to relax into a steady state, which is beyond the scope of the present study.
3.3 Limitations of the numerical model
The present simulation has employed the IBM, in which the membrane force is distributed over a band of surrounding Eulerian fluid grids (approximately
![]() $2\unicode[STIX]{x0394}x$
on each side of the membrane, according to the Dirac delta function used (Sui et al.
Reference Sui, Chew, Roy and Low2008a
)). The second-order approach used to implement the no-slip wall boundary condition in the LBM needs the values of the probability density function at fluid grid points within
$2\unicode[STIX]{x0394}x$
on each side of the membrane, according to the Dirac delta function used (Sui et al.
Reference Sui, Chew, Roy and Low2008a
)). The second-order approach used to implement the no-slip wall boundary condition in the LBM needs the values of the probability density function at fluid grid points within
![]() $2\unicode[STIX]{x0394}x$
from the wall. As a result, when the capsule membrane gets close to the wall (i.e. when the thickness of the fluid film between the membrane and the wall is comparable to
$2\unicode[STIX]{x0394}x$
from the wall. As a result, when the capsule membrane gets close to the wall (i.e. when the thickness of the fluid film between the membrane and the wall is comparable to
![]() $2\unicode[STIX]{x0394}x$
), the present method will not be able to resolve the film flow in the gap. This is likely to happen when a capsule is relatively large (
$2\unicode[STIX]{x0394}x$
), the present method will not be able to resolve the film flow in the gap. This is likely to happen when a capsule is relatively large (
![]() $a/R\geqslant 0.6$
) and is close to the bifurcation. However, the film is often thin over a very small area of the capsule membrane only, and therefore the thinness limitation may have a negligible effect on the overall path selection of the whole capsule. This question is left for future investigation and in the present study we only consider small capsules (
$a/R\geqslant 0.6$
) and is close to the bifurcation. However, the film is often thin over a very small area of the capsule membrane only, and therefore the thinness limitation may have a negligible effect on the overall path selection of the whole capsule. This question is left for future investigation and in the present study we only consider small capsules (
![]() $a/R\leqslant 0.4$
), for which this problem does not occur. It should be noted that in our validation tests presented in figure 2, the liquid film between the capsule and the tube wall has always been resolved by more than three fluid grids.
$a/R\leqslant 0.4$
), for which this problem does not occur. It should be noted that in our validation tests presented in figure 2, the liquid film between the capsule and the tube wall has always been resolved by more than three fluid grids.

Figure 4. Fluid separation lines calculated in cross-section
![]() $S_{c}$
at different Reynolds numbers and branch flow ratios. The cross-section is
$S_{c}$
at different Reynolds numbers and branch flow ratios. The cross-section is
![]() $2R$
from the entrance, where the flow remains the Poiseuille profile imposed at the inlet. In the cross-section, the fluid elements above the separation line enter the side branch and those below remain in the main tube. (a) Separation lines for flows at low Reynolds numbers. The lines correspond to the present simulation results, the ▵ symbols to the experimental results of Rong & Carr (Reference Rong and Carr1990), the
$2R$
from the entrance, where the flow remains the Poiseuille profile imposed at the inlet. In the cross-section, the fluid elements above the separation line enter the side branch and those below remain in the main tube. (a) Separation lines for flows at low Reynolds numbers. The lines correspond to the present simulation results, the ▵ symbols to the experimental results of Rong & Carr (Reference Rong and Carr1990), the
![]() $\times$
symbols to the simulation results of Enden & Popel (Reference Enden and Popel1992). (b) Separation lines for flows at
$\times$
symbols to the simulation results of Enden & Popel (Reference Enden and Popel1992). (b) Separation lines for flows at
![]() $Re=27.5$
. The full lines correspond to the present results, the ▵ symbols to the experiments of Carr & Kotha (Reference Carr and Kotha1995).
$Re=27.5$
. The full lines correspond to the present results, the ▵ symbols to the experiments of Carr & Kotha (Reference Carr and Kotha1995).
4 Flow in the branched tube without a capsule
We consider the flow in the branched tube in absence of any capsule and study the influence of the flow split ratio and Reynolds number. The results will help us analyse some features of capsule dynamics. Furthermore, the results for the background flows will be compared with previous experimental (Rong & Carr Reference Rong and Carr1990; Carr & Kotha Reference Carr and Kotha1995) and numerical (Enden & Popel Reference Enden and Popel1992) studies to further validate the present numerical model.
Within each cross-section of the parent tube perpendicular to the tube centreline, one can define a separation line that divides the fluid elements that flow into the side branch from those flowing down the straight tube. We determine the fluid separation line in the cross-section
![]() $S_{c}$
and study how it evolves as a function of the flow split ratio and Reynolds number. When a fully developed Poiseuille flow is imposed at the entrance
$S_{c}$
and study how it evolves as a function of the flow split ratio and Reynolds number. When a fully developed Poiseuille flow is imposed at the entrance
![]() $S_{0}$
, the flow remains fully developed in cross-section
$S_{0}$
, the flow remains fully developed in cross-section
![]() $S_{c}$
. In order to generate a fluid separation line, 40 000 massless and diffusiveless tracer particles are initially distributed evenly in
$S_{c}$
. In order to generate a fluid separation line, 40 000 massless and diffusiveless tracer particles are initially distributed evenly in
![]() $S_{c}$
and released. Their trajectories are calculated using an integration method that is detailed in Sui, Teo & Lee (Reference Sui, Teo and Lee2012). At the position where a particle is released, a passive scalar
$S_{c}$
and released. Their trajectories are calculated using an integration method that is detailed in Sui, Teo & Lee (Reference Sui, Teo and Lee2012). At the position where a particle is released, a passive scalar
![]() $\unicode[STIX]{x1D719}$
is defined, which takes the value of one when the particle enters the side branch and zero otherwise. The separation line is approximated by the isocontour
$\unicode[STIX]{x1D719}$
is defined, which takes the value of one when the particle enters the side branch and zero otherwise. The separation line is approximated by the isocontour
![]() $\unicode[STIX]{x1D719}=0.5$
. Less than 0.1 % of the particles are found to get trapped near the apex of the bifurcation, the effect of which can thus be neglected considering the large number of particles released.
$\unicode[STIX]{x1D719}=0.5$
. Less than 0.1 % of the particles are found to get trapped near the apex of the bifurcation, the effect of which can thus be neglected considering the large number of particles released.

Figure 5. Fluid separation lines in branched tube flows. The cross-section is the same as that in figure 4. (a) Separation lines for flows at
![]() $Re=0.25$
with different branch flow ratios; (b) separation lines for flows at different Reynolds numbers with a fixed branch flow ratio
$Re=0.25$
with different branch flow ratios; (b) separation lines for flows at different Reynolds numbers with a fixed branch flow ratio
![]() $q=0.5$
.
$q=0.5$
.
The separation lines are shown in figure 4(a) for low Reynolds number (
![]() $Re<1$
) flows for different branch flow ratios
$Re<1$
) flows for different branch flow ratios
![]() $q$
. They are compared with the experimental results of Rong & Carr (Reference Rong and Carr1990) and with the numerical simulations of Enden & Popel (Reference Enden and Popel1992), who considered Stokes flow and used a finite element method. Satisfactory agreements are found in all the cases considered. We can conclude that the flow separation line only depends on the branch flow ratio when
$q$
. They are compared with the experimental results of Rong & Carr (Reference Rong and Carr1990) and with the numerical simulations of Enden & Popel (Reference Enden and Popel1992), who considered Stokes flow and used a finite element method. Satisfactory agreements are found in all the cases considered. We can conclude that the flow separation line only depends on the branch flow ratio when
![]() $Re<1$
. We also compare the flow separation lines calculated at a higher Reynolds number (
$Re<1$
. We also compare the flow separation lines calculated at a higher Reynolds number (
![]() $Re=27.5$
) with the experiments of Carr & Kotha (Reference Carr and Kotha1995) under different flow splits in figure 4(b). Reasonably good agreement is again achieved. Note that
$Re=27.5$
) with the experiments of Carr & Kotha (Reference Carr and Kotha1995) under different flow splits in figure 4(b). Reasonably good agreement is again achieved. Note that
![]() $Re$
in Carr & Kotha (Reference Carr and Kotha1995) was defined using the maximum flow velocity.
$Re$
in Carr & Kotha (Reference Carr and Kotha1995) was defined using the maximum flow velocity.
We can also build the lines for flows at a fixed Reynolds number but different branch flow ratios. The results are presented in figure 5(a) for
![]() $Re=0.25$
. At equal flow split (
$Re=0.25$
. At equal flow split (
![]() $q=0.5$
), the separation line is almost flat and equally divides the cross-sectional area. However, when the branch flow ratio increases (respectively decreases) from 0.5, the separation line moves and bends downwards (respectively upwards).
$q=0.5$
), the separation line is almost flat and equally divides the cross-sectional area. However, when the branch flow ratio increases (respectively decreases) from 0.5, the separation line moves and bends downwards (respectively upwards).
Figure 5(b) presents the separation lines for a fixed flow split ratio
![]() $q=0.5$
but different flow Reynolds numbers. When the Reynolds number is increased, the fluid separation line bends towards the side branch. We will later discuss the effect of the geometry of the separation line on the path that the capsule selects.
$q=0.5$
but different flow Reynolds numbers. When the Reynolds number is increased, the fluid separation line bends towards the side branch. We will later discuss the effect of the geometry of the separation line on the path that the capsule selects.
5 Flow of a capsule in a branched tube
We first present in § 5.1 the three-dimensional flow results for a capsule at small Reynolds number flow, for which inertial effects are negligible.
The objective is to set-up a reference for the study of the effect of inertia. The effect of
![]() $Re$
is then considered in § 5.2, by increasing the flow strength. We show how the tendency of the capsule to flow into the side branch changes with the flow strength, capsule size and membrane elasticity and provide a phase diagram of the capsule path selection in § 5.3.
$Re$
is then considered in § 5.2, by increasing the flow strength. We show how the tendency of the capsule to flow into the side branch changes with the flow strength, capsule size and membrane elasticity and provide a phase diagram of the capsule path selection in § 5.3.

Figure 6. Effect of branch flow ratio
![]() $q$
on the capsule trajectories (
$q$
on the capsule trajectories (
![]() $R=0.4$
,
$R=0.4$
,
![]() $Re=0.25$
,
$Re=0.25$
,
![]() $Ca=0.5$
). The triangle denotes the position where the bifurcation starts to affect the capsule motion. The squares label the centre of mass positions where the capsule maximum principal tension are the largest (see figure 9).
$Ca=0.5$
). The triangle denotes the position where the bifurcation starts to affect the capsule motion. The squares label the centre of mass positions where the capsule maximum principal tension are the largest (see figure 9).
5.1 Effect of flow split ratio (
 $Re<1$
)
$Re<1$
)
We start from a capsule with a size ratio
![]() $a/R=0.4$
and
$a/R=0.4$
and
![]() $Ca=0.5$
at different branch flow ratios. The Reynolds number based on the parent tube is 0.25. Figure 6 presents the trajectories of the capsule centre of mass for different branch flow ratios. We recover the fact that the capsule favours the branch with the higher flow rate (Barber et al.
Reference Barber, Alberding, Restrepo and Secomb2008; Woolfenden & Blyth Reference Woolfenden and Blyth2011): as the capsule approaches the bifurcation, it slows down, is first attracted by the side branch and flows into it if
$Ca=0.5$
at different branch flow ratios. The Reynolds number based on the parent tube is 0.25. Figure 6 presents the trajectories of the capsule centre of mass for different branch flow ratios. We recover the fact that the capsule favours the branch with the higher flow rate (Barber et al.
Reference Barber, Alberding, Restrepo and Secomb2008; Woolfenden & Blyth Reference Woolfenden and Blyth2011): as the capsule approaches the bifurcation, it slows down, is first attracted by the side branch and flows into it if
![]() $q$
is large enough (
$q$
is large enough (
![]() $q\geqslant 0.5$
in this case). Otherwise, it migrates back towards the centreline of the straight tube after passing the bifurcation region. In both cases, the capsule does not reach its equilibrium shape when approaching the exit as discussed in § 3.2.
$q\geqslant 0.5$
in this case). Otherwise, it migrates back towards the centreline of the straight tube after passing the bifurcation region. In both cases, the capsule does not reach its equilibrium shape when approaching the exit as discussed in § 3.2.

Figure 7. Effect of flow split ratio on the path selection of a capsule (
![]() $a/R=0.4$
,
$a/R=0.4$
,
![]() $Re=0.25$
,
$Re=0.25$
,
![]() $Ca=0.5$
). The profiles are plotted in the
$Ca=0.5$
). The profiles are plotted in the
![]() $xz$
-plane. The black dots are attached to two material points of the capsule membrane. The profiles are shown at
$xz$
-plane. The black dots are attached to two material points of the capsule membrane. The profiles are shown at
![]() $Vt/R=4.16$
, 4.8, 5.44, 6.08, 6.72, 8, 9.28, 10.56, 11.84. (a)
$Vt/R=4.16$
, 4.8, 5.44, 6.08, 6.72, 8, 9.28, 10.56, 11.84. (a)
![]() $q=0.6$
, (b)
$q=0.6$
, (b)
![]() $q=0.4$
.
$q=0.4$
.

Figure 8. Capsule in the branched tube at different branch flow ratios (
![]() $a/R=0.4$
,
$a/R=0.4$
,
![]() $Re=0.25$
,
$Re=0.25$
,
![]() $Ca=0.5$
). Time evolution of (a) the velocity magnitude
$Ca=0.5$
). Time evolution of (a) the velocity magnitude
![]() $V_{c}/V$
, and of (b) the maximum principal tension. The squares indicate the dimensionless times when
$V_{c}/V$
, and of (b) the maximum principal tension. The squares indicate the dimensionless times when
![]() $\unicode[STIX]{x1D70F}_{max}$
reaches its peak value. The corresponding positions of the capsule centre of mass are shown in figure 6. The triangle denotes the position where the bifurcation starts to affect the capsule motion.
$\unicode[STIX]{x1D70F}_{max}$
reaches its peak value. The corresponding positions of the capsule centre of mass are shown in figure 6. The triangle denotes the position where the bifurcation starts to affect the capsule motion.
We now investigate the motion and deformation of the capsule near the bifurcation region at different flow splits. Before entering the bifurcation region, the capsule has a parachute shape in the parent tube (figure 7
a,b). The capsule shape starts to deviate from the steady profile when it is about one diameter from the junction (position marked by a triangle in figure 6). The successive profiles of the capsule in the bifurcation vicinity are shown in figure 7 for two different flow split ratios (
![]() $q=0.4$
and 0.6). Two membrane material points initially located at the upper and lower sides of the capsule are marked with black dots to facilitate the visualization of the membrane motion. In both cases the capsule first moves upwards towards the side branch, loses its symmetric shape and becomes elongated along the branch flow direction. The capsule enters the side branch for
$q=0.4$
and 0.6). Two membrane material points initially located at the upper and lower sides of the capsule are marked with black dots to facilitate the visualization of the membrane motion. In both cases the capsule first moves upwards towards the side branch, loses its symmetric shape and becomes elongated along the branch flow direction. The capsule enters the side branch for
![]() $q=0.6$
(figure 7
a), while it remains in the straight tube for
$q=0.6$
(figure 7
a), while it remains in the straight tube for
![]() $q=0.4$
(figure 7
b). In both cases, once the capsule has entered either one of the tubes, it is off-centred from the channel axis. It therefore undergoes a clockwise (respectively counterclockwise) tank-treading motion during its migration towards the centreline of the side branch (respectively straight tube), as can be seen from the trajectory of the tracker dots attached to the capsule membrane.
$q=0.4$
(figure 7
b). In both cases, once the capsule has entered either one of the tubes, it is off-centred from the channel axis. It therefore undergoes a clockwise (respectively counterclockwise) tank-treading motion during its migration towards the centreline of the side branch (respectively straight tube), as can be seen from the trajectory of the tracker dots attached to the capsule membrane.
In the parent tube before the bifurcation region, the capsule flows at a steady speed, which is higher than the average speed of the flow (a signature of the Fåhraeus effect (Fåhraeus Reference Fåhraeus1929)). The steady speed of the capsule with
![]() $a/R=0.4$
decreases slightly with the capillary number (not shown), which is consistent with the results of Lefebvre et al. (Reference Lefebvre, Leclerc, Barthès-Biesel, Walter and Edwards-Lévy2008) obtained for a capsule in a straight cylindrical channel at confinement ratios
$a/R=0.4$
decreases slightly with the capillary number (not shown), which is consistent with the results of Lefebvre et al. (Reference Lefebvre, Leclerc, Barthès-Biesel, Walter and Edwards-Lévy2008) obtained for a capsule in a straight cylindrical channel at confinement ratios
![]() $a/R\geqslant 0.8$
. When the capsule approaches the bifurcation, it encounters a relatively high pressure: it is thus flattened (as evidenced by the profiles at
$a/R\geqslant 0.8$
. When the capsule approaches the bifurcation, it encounters a relatively high pressure: it is thus flattened (as evidenced by the profiles at
![]() $Vt/R=5.44$
and 6.08). Its speed
$Vt/R=5.44$
and 6.08). Its speed
![]() $V_{c}$
correspondingly decreases to a minimum and then increases back towards a steady value determined by the flow rate in the corresponding downstream tube (figure 8
a).
$V_{c}$
correspondingly decreases to a minimum and then increases back towards a steady value determined by the flow rate in the corresponding downstream tube (figure 8
a).
The maximum principal elastic tension in the membrane
![]() $\unicode[STIX]{x1D70F}_{max}=\max [\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2}]$
, where
$\unicode[STIX]{x1D70F}_{max}=\max [\unicode[STIX]{x1D70F}_{1},\unicode[STIX]{x1D70F}_{2}]$
, where
![]() $\unicode[STIX]{x1D70F}_{1}$
and
$\unicode[STIX]{x1D70F}_{1}$
and
![]() $\unicode[STIX]{x1D70F}_{2}$
are calculated from (2.2), is a relevant quantity to evaluate the likelihood of membrane rupture.
$\unicode[STIX]{x1D70F}_{2}$
are calculated from (2.2), is a relevant quantity to evaluate the likelihood of membrane rupture.
Figure 8(b) shows that
![]() $\unicode[STIX]{x1D70F}_{max}$
increases significantly when the capsule approaches the bifurcation. Note that the velocity decrease is almost equal for conditions
$\unicode[STIX]{x1D70F}_{max}$
increases significantly when the capsule approaches the bifurcation. Note that the velocity decrease is almost equal for conditions
![]() $q=0.6$
and 0.4, and for
$q=0.6$
and 0.4, and for
![]() $q=0.7$
and 0.3. However, for equal flow split (
$q=0.7$
and 0.3. However, for equal flow split (
![]() $q=0.5$
), there is a strong decrease in velocity and a large increase in capsule deformation and elastic tension in the membrane. The deformed profiles of the capsules corresponding to the peak of
$q=0.5$
), there is a strong decrease in velocity and a large increase in capsule deformation and elastic tension in the membrane. The deformed profiles of the capsules corresponding to the peak of
![]() $\unicode[STIX]{x1D70F}_{max}$
are shown in figure 9: the initially spherical capsule is significantly deformed. A black dot shows where the peak is reached: the maximum tension occurs where the viscous shear stress exerted by the suspending fluid changes sign.
$\unicode[STIX]{x1D70F}_{max}$
are shown in figure 9: the initially spherical capsule is significantly deformed. A black dot shows where the peak is reached: the maximum tension occurs where the viscous shear stress exerted by the suspending fluid changes sign.
5.2 Effect of flow strength and size ratio
We now turn to the effect of flow strength on the path selection of a capsule for flow regimes where inertia is not negligible. The fluid properties (
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D707}$
), the capsule size (
$\unicode[STIX]{x1D707}$
), the capsule size (
![]() $a/R=0.4$
) and the membrane properties (
$a/R=0.4$
) and the membrane properties (
![]() $G_{s}$
) are fixed. Thus increasing the mean flow speed simultaneously increases the flow Reynolds number and the capillary number. The combined effect of these two parameters is unknown. We first consider the case
$G_{s}$
) are fixed. Thus increasing the mean flow speed simultaneously increases the flow Reynolds number and the capillary number. The combined effect of these two parameters is unknown. We first consider the case
![]() $Ca=0.005Re$
, for which
$Ca=0.005Re$
, for which
![]() $Ca$
evolves from a very small value up to 0.2 for the highest flow strength corresponding to
$Ca$
evolves from a very small value up to 0.2 for the highest flow strength corresponding to
![]() $Re=40$
.
$Re=40$
.

Figure 9. Capsule profiles in the
![]() $xz$
-plane when the maximum principal tension reaches its peak (
$xz$
-plane when the maximum principal tension reaches its peak (
![]() $a/R=0.4$
,
$a/R=0.4$
,
![]() $Re=0.25$
,
$Re=0.25$
,
![]() $Ca=0.5$
). The black dots show where the principal tension is maximum.
$Ca=0.5$
). The black dots show where the principal tension is maximum.

Figure 10. Effect of flow strength on the capsule trajectory in the symmetric
![]() $xz$
-plane (
$xz$
-plane (
![]() $a/R=0.4$
,
$a/R=0.4$
,
![]() $q=0.52$
). (a)
$q=0.52$
). (a)
![]() $Re=1$
,
$Re=1$
,
![]() $Ca=0.005$
; (b)
$Ca=0.005$
; (b)
![]() $Re=40$
,
$Re=40$
,
![]() $Ca=0.2$
. The thick solid line represents the trajectory of the capsule centre. The dark line with arrows (shown in red online) represents the centre streamline of the undisturbed background flow, while the grey line with arrows (shown in green online) represents the separating streamline that divides the fluid elements entering the side branch from ones entering the downstream main tube.
$Ca=0.2$
. The thick solid line represents the trajectory of the capsule centre. The dark line with arrows (shown in red online) represents the centre streamline of the undisturbed background flow, while the grey line with arrows (shown in green online) represents the separating streamline that divides the fluid elements entering the side branch from ones entering the downstream main tube.
The trajectories of the capsule centre of mass and some instantaneous profiles are shown in figure 10 for two different Reynolds numbers and
![]() $q=0.52$
. It is useful to compare the relative positions in the symmetric
$q=0.52$
. It is useful to compare the relative positions in the symmetric
![]() $xz$
-plane of the capsule centre trajectory, the unperturbed centre streamline (emanating from the centre of
$xz$
-plane of the capsule centre trajectory, the unperturbed centre streamline (emanating from the centre of
![]() $S_{c}$
in absence of a capsule) and the unperturbed separating streamline (dividing the fluid elements that enter the side branch from those that enter the straight tube). At low mean flow speed (
$S_{c}$
in absence of a capsule) and the unperturbed separating streamline (dividing the fluid elements that enter the side branch from those that enter the straight tube). At low mean flow speed (
![]() $Re=1$
), the capsule essentially keeps its spherical shape because
$Re=1$
), the capsule essentially keeps its spherical shape because
![]() $Ca=0.005$
is very small. Its trajectory follows the unperturbed centre streamline until it is close to the bifurcation, but deviates from it due to wall exclusion effects inside the side branch. At high flow speed (
$Ca=0.005$
is very small. Its trajectory follows the unperturbed centre streamline until it is close to the bifurcation, but deviates from it due to wall exclusion effects inside the side branch. At high flow speed (
![]() $Re=40$
), the capillary number is fairly large (
$Re=40$
), the capillary number is fairly large (
![]() $Ca=0.2$
) and the capsule is significantly deformed. Its trajectory first deviates a little from the background streamline moving slightly towards the side branch, but eventually remains in the main tube (like the centre streamline). Therefore increasing the flow speed and thus inertial effect, tends to keep the capsule flowing straight in the main tube. The relative position between the separating streamline and the centre streamline seems to play an important role. Indeed, for
$Ca=0.2$
) and the capsule is significantly deformed. Its trajectory first deviates a little from the background streamline moving slightly towards the side branch, but eventually remains in the main tube (like the centre streamline). Therefore increasing the flow speed and thus inertial effect, tends to keep the capsule flowing straight in the main tube. The relative position between the separating streamline and the centre streamline seems to play an important role. Indeed, for
![]() $Re=1$
, the separation streamline is initially slightly below the centreline of the parent tube: the centre streamline (and the capsule) thus goes into the side branch. Conversely, for
$Re=1$
, the separation streamline is initially slightly below the centreline of the parent tube: the centre streamline (and the capsule) thus goes into the side branch. Conversely, for
![]() $Re=40$
, the separating streamline is initially above the centreline of the parent tube: the centre streamline (and the capsule) thus goes into the straight tube.
$Re=40$
, the separating streamline is initially above the centreline of the parent tube: the centre streamline (and the capsule) thus goes into the straight tube.

Figure 11. Effect of capsule size on its trajectory for
![]() $Re=20$
,
$Re=20$
,
![]() $q=0.56$
,
$q=0.56$
,
![]() $Ca=0.1$
: (a)
$Ca=0.1$
: (a)
![]() $a/R=0.4$
, (b)
$a/R=0.4$
, (b)
![]() $a/R=0.2$
. The streamline legend is the same as in figure 10.
$a/R=0.2$
. The streamline legend is the same as in figure 10.
For given values of
![]() $Re$
,
$Re$
,
![]() $Ca$
and
$Ca$
and
![]() $q$
, the capsule trajectory depends on the size ratio
$q$
, the capsule trajectory depends on the size ratio
![]() $a/R$
. If a capsule has a negligible size and is non-diffusive (i.e. negligible Brownian motion), we expect that it will follow the centre streamline. However, the path selection of a finite size capsule remains an open question. As shown in figure 11, for
$a/R$
. If a capsule has a negligible size and is non-diffusive (i.e. negligible Brownian motion), we expect that it will follow the centre streamline. However, the path selection of a finite size capsule remains an open question. As shown in figure 11, for
![]() $q=0.56$
, a small capsule (
$q=0.56$
, a small capsule (
![]() $a/R=0.2$
) flows into the straight tube, whereas a large one (
$a/R=0.2$
) flows into the straight tube, whereas a large one (
![]() $a/R=0.4$
) flows into the side branch. This phenomenon may be partly attributed to the capsule deformation, which can be quantified by means of the stored elastic energy
$a/R=0.4$
) flows into the side branch. This phenomenon may be partly attributed to the capsule deformation, which can be quantified by means of the stored elastic energy
![]() $E(t)$
, given by
$E(t)$
, given by
where
![]() $W^{SK}$
is given by (2.1) and
$W^{SK}$
is given by (2.1) and
![]() $A_{0}$
is the initial surface area of the capsule.
$A_{0}$
is the initial surface area of the capsule.
When the capsule is in the bifurcation region, the maximum of the stored elastic energy, normalized by
![]() $a^{2}G_{s}$
, drops from 0.91 to 0.2 when the size of the capsule decreases from
$a^{2}G_{s}$
, drops from 0.91 to 0.2 when the size of the capsule decreases from
![]() $0.4R$
to
$0.4R$
to
![]() $0.2R$
. This means that the smaller capsule is less deformed than the larger one. This is due to the fact that the shear rate varies across the tube and that the effective capillary number to which the capsule is subjected is then
$0.2R$
. This means that the smaller capsule is less deformed than the larger one. This is due to the fact that the shear rate varies across the tube and that the effective capillary number to which the capsule is subjected is then
![]() $Ca\times a/R$
, rather than just
$Ca\times a/R$
, rather than just
![]() $Ca$
. As the smaller capsule is less deformed, its centre does not deviate much from the centre streamline: the capsule follows it into the straight tube in this case (
$Ca$
. As the smaller capsule is less deformed, its centre does not deviate much from the centre streamline: the capsule follows it into the straight tube in this case (
![]() $q=0.56$
). The larger capsule, however, deviates from the centre streamline and is attracted into the side branch. We find that the background flow also plays an important role in path selection of capsules with different sizes, as it will be discussed in § 6.1.
$q=0.56$
). The larger capsule, however, deviates from the centre streamline and is attracted into the side branch. We find that the background flow also plays an important role in path selection of capsules with different sizes, as it will be discussed in § 6.1.
5.3 Path selection phase diagram
A simple way to characterize path selection of a capsule is to define the critical branch flow ratio
![]() $q_{c}$
, above which the capsule enters the side branch: the capsule thus flows in the straight tube if
$q_{c}$
, above which the capsule enters the side branch: the capsule thus flows in the straight tube if
![]() $q<q_{c}$
, and in the side branch otherwise. For given values of
$q<q_{c}$
, and in the side branch otherwise. For given values of
![]() $Re$
and
$Re$
and
![]() $Ca$
, we progressively increase
$Ca$
, we progressively increase
![]() $q$
from 0.1 by large steps
$q$
from 0.1 by large steps
![]() $\unicode[STIX]{x0394}q=0.05$
until we find the transition, where the capsule flows into the side branch rather than the straight tube. We then refine the step to
$\unicode[STIX]{x0394}q=0.05$
until we find the transition, where the capsule flows into the side branch rather than the straight tube. We then refine the step to
![]() $\unicode[STIX]{x0394}q=0.02$
around the transition region. The value of
$\unicode[STIX]{x0394}q=0.02$
around the transition region. The value of
![]() $q_{c}$
is taken as the average of the two successive branch flow ratios
$q_{c}$
is taken as the average of the two successive branch flow ratios
![]() $q$
wherein the capsule enters the side branch for the largest or remains in the main tube for the smallest. Therefore
$q$
wherein the capsule enters the side branch for the largest or remains in the main tube for the smallest. Therefore
![]() $q_{c}$
is determined within
$q_{c}$
is determined within
![]() $\pm 0.01$
. Near the transition, we have conducted tests using finer grid resolutions (
$\pm 0.01$
. Near the transition, we have conducted tests using finer grid resolutions (
![]() $\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=\unicode[STIX]{x0394}z=0.031R$
) and found that the trajectories of the capsule remain unchanged.
$\unicode[STIX]{x0394}x=\unicode[STIX]{x0394}y=\unicode[STIX]{x0394}z=0.031R$
) and found that the trajectories of the capsule remain unchanged.

Figure 12. Phase diagram: critical branch flow ratio as a function of the tube Reynolds number for capsules with different sizes and membrane shear elasticity. For
![]() $q>q_{c}$
, the capsule flows into the side branch.
$q>q_{c}$
, the capsule flows into the side branch.
The critical branch flow ratio is shown in figure 12 as a function of the flow Reynolds number for capsules with different sizes and membrane shear elasticity. In the extreme case of an infinitely small capsule (i.e.
![]() $a/R=0$
), the capsule follows the unperturbed streamline. For low inertia (
$a/R=0$
), the capsule follows the unperturbed streamline. For low inertia (
![]() $Re=0.25$
),
$Re=0.25$
),
![]() $q_{c}=0.48\sim 0.49$
, which means that the capsule tends to favour the side branch when the flow split is even. This is what we observe for
$q_{c}=0.48\sim 0.49$
, which means that the capsule tends to favour the side branch when the flow split is even. This is what we observe for
![]() $Ca/Re=0.005$
or 0.02, where the capsule is only slightly deformed and behaves as a solid sphere (
$Ca/Re=0.005$
or 0.02, where the capsule is only slightly deformed and behaves as a solid sphere (
![]() $Ca=0.0013$
or 0.005). Interestingly, this still occurs in the case
$Ca=0.0013$
or 0.005). Interestingly, this still occurs in the case
![]() $Ca/Re=2$
(
$Ca/Re=2$
(
![]() $Ca=0.5$
– pink diamond in figure 12), even though the capsule is quite deformed under these conditions as can be surmised from figure 7. This is consistent with the two-dimensional simulation by Woolfenden & Blyth (Reference Woolfenden and Blyth2011) in Stokes flow. For
$Ca=0.5$
– pink diamond in figure 12), even though the capsule is quite deformed under these conditions as can be surmised from figure 7. This is consistent with the two-dimensional simulation by Woolfenden & Blyth (Reference Woolfenden and Blyth2011) in Stokes flow. For
![]() $Re>1$
,
$Re>1$
,
![]() $q_{c}$
increases significantly when
$q_{c}$
increases significantly when
![]() $Re$
increases and the capsule size ratio decreases. Up to
$Re$
increases and the capsule size ratio decreases. Up to
![]() $Re\leqslant 4$
, the main effect on
$Re\leqslant 4$
, the main effect on
![]() $q_{c}$
is only due to size ratio and thus to confinement of the capsule by the tube. The influence of capsule deformability becomes significant at larger flow rates corresponding to
$q_{c}$
is only due to size ratio and thus to confinement of the capsule by the tube. The influence of capsule deformability becomes significant at larger flow rates corresponding to
![]() $Re\geqslant 10$
.
$Re\geqslant 10$
.
6 Discussion and conclusion
We have studied the three-dimensional flow of an initially spherical capsule through a straight tube with a right-angled side branch, using an immersed-boundary lattice Boltzmann method. This flow configuration is interesting as it leads to non-symmetric flow conditions between the two branches, contrary to the classical T-junction that is equivalent in terms of geometry and has received great attention. The study allows to elucidate the effects of flow split ratio, flow strength and capsule size ratio (
![]() $a/R\leqslant 0.4$
) on the capsule path selection at the bifurcation. It also provides us with information on the capsule deformation and corresponding stress level in the membrane.
$a/R\leqslant 0.4$
) on the capsule path selection at the bifurcation. It also provides us with information on the capsule deformation and corresponding stress level in the membrane.
The path selection results are well summarized by means of the critical branch flow ratio
![]() $q_{c}$
, which is the lower bound of the flow split ratio
$q_{c}$
, which is the lower bound of the flow split ratio
![]() $q$
, for which the capsule enters the side branch.
$q$
, for which the capsule enters the side branch.
For low Reynolds numbers, the critical branch flow ratio is very slightly below 0.5, which means that the capsule favours the side branch at equal flow split, but otherwise takes a path which is essentially determined by the value of
![]() $q$
. This result is qualitatively consistent with the earlier numerical study of Woolfenden & Blyth (Reference Woolfenden and Blyth2011). However the authors used a two-dimensional model and a simple generalized Hooke’s law for the membrane, which renders impossible any quantitative comparison.
$q$
. This result is qualitatively consistent with the earlier numerical study of Woolfenden & Blyth (Reference Woolfenden and Blyth2011). However the authors used a two-dimensional model and a simple generalized Hooke’s law for the membrane, which renders impossible any quantitative comparison.
We also consider flows with significant inertial effects, which had not been studied before. Such flows are encountered in fast flowing microfluidic devices (Di Carlo et al.
Reference Di Carlo, Irimia, Tompkins and Toner2007) or when millimetric capsules flow in fairly large capillary tubes. We find that the critical branch flow ratio is then larger than 0.5 and increases significantly with the Reynolds number, when
![]() $Re\geqslant 10$
. However,
$Re\geqslant 10$
. However,
![]() $q_{c}$
tends to decrease when the capsule size and/or deformation increase. This indicates that at equal flow split, the capsule tends to flow straight in the main tube when inertial effects are significant. This is a consequence of the effects of inertia on the background flow in the branched tube, which alters the shape of the fluid separation line in the upstream cross-section
$q_{c}$
tends to decrease when the capsule size and/or deformation increase. This indicates that at equal flow split, the capsule tends to flow straight in the main tube when inertial effects are significant. This is a consequence of the effects of inertia on the background flow in the branched tube, which alters the shape of the fluid separation line in the upstream cross-section
![]() $S_{c}$
, as discussed in details in the following § 6.1.
$S_{c}$
, as discussed in details in the following § 6.1.

Figure 13. (a) Illustration for the definition of the momentum ratio. The dash line is a fluid separation line (for
![]() $q=0.5$
,
$q=0.5$
,
![]() $Re=20$
), which divides the cross-sectional area of the capsule (shaded circle) into two regions (
$Re=20$
), which divides the cross-sectional area of the capsule (shaded circle) into two regions (
![]() $S_{b}$
and
$S_{b}$
and
![]() $S_{m}$
) covered by fluid elements that finally enter the side branch and downstream main tube, respectively. Momentum ratios of capsules with
$S_{m}$
) covered by fluid elements that finally enter the side branch and downstream main tube, respectively. Momentum ratios of capsules with
![]() $a/R=0.2$
and 0.4 as a function of (b)
$a/R=0.2$
and 0.4 as a function of (b)
![]() $q$
at
$q$
at
![]() $Re=0.25$
, (c)
$Re=0.25$
, (c)
![]() $Re$
at
$Re$
at
![]() $q=0.5$
.
$q=0.5$
.
6.1 Background flow momentum split: a simple model of path selection
All the above results have been obtained with the full fluid–structure interaction model, which is quite intricate and necessitates long computations. It is of interest to consider a much simpler model, based on the interaction of the background flow with the undeformed capsule, and investigate the validity limits of this model by comparing the predictions to the ones provided by the full model.
In this simple model, we assume that the presence of the capsule does not change the background flow significantly, and evaluate the interaction between the undeformed capsule and the unperturbed flow in section
![]() $S_{c}$
. The model is based on the ascertainment that the cross-sectional area of the capsule (the shadowed area in figure 13
a) in the plane
$S_{c}$
. The model is based on the ascertainment that the cross-sectional area of the capsule (the shadowed area in figure 13
a) in the plane
![]() $S_{c}$
is divided by the fluid separation line (§ 4) into two distinct regions,
$S_{c}$
is divided by the fluid separation line (§ 4) into two distinct regions,
![]() $S_{b}$
and
$S_{b}$
and
![]() $S_{m}$
, having fluid elements that, respectively, enter the side branch and the downstream main tube eventually (figure 13
a). We then define the ratio
$S_{m}$
, having fluid elements that, respectively, enter the side branch and the downstream main tube eventually (figure 13
a). We then define the ratio
![]() $M$
between the momentum of the fluid elements in
$M$
between the momentum of the fluid elements in
![]() $S_{b}$
and the total momentum of fluid elements in the cross-sectional area of the capsule
$S_{b}$
and the total momentum of fluid elements in the cross-sectional area of the capsule
![]() $S_{b}+S_{m}$
:
$S_{b}+S_{m}$
:
 $$\begin{eqnarray}M=\frac{\displaystyle \int _{S_{b}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{b}}{\displaystyle \int _{S_{b}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{b}+\int _{S_{m}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{m}},\end{eqnarray}$$
$$\begin{eqnarray}M=\frac{\displaystyle \int _{S_{b}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{b}}{\displaystyle \int _{S_{b}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{b}+\int _{S_{m}}\unicode[STIX]{x1D70C}u(y,z)\,\text{d}S_{m}},\end{eqnarray}$$
where
![]() $u(y,z)$
is the fluid velocity along the
$u(y,z)$
is the fluid velocity along the
![]() $x$
-direction in
$x$
-direction in
![]() $S_{c}$
. We then assume that for
$S_{c}$
. We then assume that for
![]() $M>0.5$
, the capsule enters the side branch. The evolution of
$M>0.5$
, the capsule enters the side branch. The evolution of
![]() $M$
with flow split
$M$
with flow split
![]() $q$
at low
$q$
at low
![]() $Re$
is shown in figure 13(b), while the effect of
$Re$
is shown in figure 13(b), while the effect of
![]() $Re$
on
$Re$
on
![]() $M$
at equal flow split
$M$
at equal flow split
![]() $q=0.5$
is shown in figure 13(c).
$q=0.5$
is shown in figure 13(c).
At equal flow split
![]() $q=0.5$
and for low Reynolds number (
$q=0.5$
and for low Reynolds number (
![]() $Re=0.25$
),
$Re=0.25$
),
![]() $M$
is slightly larger than 0.5 for both capsules (see insert of figure 13
b), suggesting that the slight momentum unbalance of the background flow helps send the capsule into the side branch. This is consistent with the predictions of the phase diagram, wherein
$M$
is slightly larger than 0.5 for both capsules (see insert of figure 13
b), suggesting that the slight momentum unbalance of the background flow helps send the capsule into the side branch. This is consistent with the predictions of the phase diagram, wherein
![]() $q_{c}$
is below 0.5 for both capsules. Similarly, for
$q_{c}$
is below 0.5 for both capsules. Similarly, for
![]() $q>0.5$
(respectively
$q>0.5$
(respectively
![]() $q<0.5$
), the momentum is
$q<0.5$
), the momentum is
![]() $M>0.5$
(respectively
$M>0.5$
(respectively
![]() $M<0.5$
) and the capsule flows into the side (respectively main) branch. This corresponds to the full model results shown in figure 6. For
$M<0.5$
) and the capsule flows into the side (respectively main) branch. This corresponds to the full model results shown in figure 6. For
![]() $q=0.5$
, an increase of
$q=0.5$
, an increase of
![]() $Re$
leads to a decrease of
$Re$
leads to a decrease of
![]() $M$
: this means that the background flow tends to push the capsule into the main branch (figure 13
c), as predicted by the phase diagram. A qualitatively similar effect is also found with the full model, as shown in figure 10. Note that the evolution of
$M$
: this means that the background flow tends to push the capsule into the main branch (figure 13
c), as predicted by the phase diagram. A qualitatively similar effect is also found with the full model, as shown in figure 10. Note that the evolution of
![]() $M$
with either
$M$
with either
![]() $q$
or
$q$
or
![]() $Re$
is qualitatively the same for the two size ratios. In figure 13(c), it is seen that when
$Re$
is qualitatively the same for the two size ratios. In figure 13(c), it is seen that when
![]() $Re\geqslant 1$
, the momentum ratio for a larger capsule is higher than that of a smaller capsule. This is one of the phenomena that predominantly accounts for the fact that, at the same flow split, a larger capsule enters the side branch, while a smaller one chooses the downstream main tube, as seen in figure 11.
$Re\geqslant 1$
, the momentum ratio for a larger capsule is higher than that of a smaller capsule. This is one of the phenomena that predominantly accounts for the fact that, at the same flow split, a larger capsule enters the side branch, while a smaller one chooses the downstream main tube, as seen in figure 11.

Figure 14. Phase diagram: critical branch flow ratio as a function of the tube Reynolds number for capsules with
![]() $a/R=0.2$
and 0.4,
$a/R=0.2$
and 0.4,
![]() $Ca/Re=0.005$
. Solid lines: full fluid–structure simulations with a capsule (see figure 12); dash lines:
$Ca/Re=0.005$
. Solid lines: full fluid–structure simulations with a capsule (see figure 12); dash lines:
![]() $q_{cm}$
from the background flow only.
$q_{cm}$
from the background flow only.
In order to quantify precisely the predictive power of the background flow momentum ratio on the path selection of a capsule, we define a critical branch flow ratio
![]() $q_{cm}$
, that corresponds to
$q_{cm}$
, that corresponds to
![]() $M=0.5$
. The value of
$M=0.5$
. The value of
![]() $q_{cm}$
is then computed as the average of the two successive branch flow ratios between which the value of
$q_{cm}$
is then computed as the average of the two successive branch flow ratios between which the value of
![]() $M$
crosses 0.5. It is determined within
$M$
crosses 0.5. It is determined within
![]() $\pm 0.01$
. The values of
$\pm 0.01$
. The values of
![]() $q_{cm}$
for capsules with
$q_{cm}$
for capsules with
![]() $a/R=0.2$
and 0.4,
$a/R=0.2$
and 0.4,
![]() $Ca/Re=0.005$
or 0.02 are shown in figure 14 and are compared with the values of
$Ca/Re=0.005$
or 0.02 are shown in figure 14 and are compared with the values of
![]() $q_{c}$
obtained from the full fluid–structure interaction simulations with the capsule. For small capsules (
$q_{c}$
obtained from the full fluid–structure interaction simulations with the capsule. For small capsules (
![]() $a/R\leqslant 0.2$
) or low inertia (
$a/R\leqslant 0.2$
) or low inertia (
![]() $Re\leqslant 4$
), the values of
$Re\leqslant 4$
), the values of
![]() $q_{c}$
and
$q_{c}$
and
![]() $q_{cm}$
are almost equal within the determination error. This indicates that the simple model, based on the momentum ratio of the undeformed capsule, is then sufficient to determine the path selection of the capsule. While this is to be expected for small capsules, it is interesting that this is also true for relatively large ones with
$q_{cm}$
are almost equal within the determination error. This indicates that the simple model, based on the momentum ratio of the undeformed capsule, is then sufficient to determine the path selection of the capsule. While this is to be expected for small capsules, it is interesting that this is also true for relatively large ones with
![]() $a/R=0.4$
. However, in this case, the values of
$a/R=0.4$
. However, in this case, the values of
![]() $q_{c}$
and
$q_{c}$
and
![]() $q_{cm}$
begin to diverge significantly for
$q_{cm}$
begin to diverge significantly for
![]() $Re\geqslant 10$
. One reason for the divergence is that the deviation of the capsule trajectory from the background flow (migration across streamlines) is mainly a result of the capsule deformability. In figure 14, the more deformable capsule (inverted triangles with solid line) deviates more than the stiffer capsule (circles with solid line) from the background flow results (circles with dash line). This can be seen from figure 15, where the capsule membrane shear elasticity leads to different flow trajectories under the same background flow condition. This means that the simple model can no longer be used to accurately compute the capsule path when the capsule deformation is significant. For example, the case shown in figure 11(a), corresponds to
$Re\geqslant 10$
. One reason for the divergence is that the deviation of the capsule trajectory from the background flow (migration across streamlines) is mainly a result of the capsule deformability. In figure 14, the more deformable capsule (inverted triangles with solid line) deviates more than the stiffer capsule (circles with solid line) from the background flow results (circles with dash line). This can be seen from figure 15, where the capsule membrane shear elasticity leads to different flow trajectories under the same background flow condition. This means that the simple model can no longer be used to accurately compute the capsule path when the capsule deformation is significant. For example, the case shown in figure 11(a), corresponds to
![]() $q=0.56$
and
$q=0.56$
and
![]() $Re=20$
. According to the value
$Re=20$
. According to the value
![]() $q_{cm}=0.57$
, the capsule should flow straight in the main tube, whereas it goes into the branch: this means that the simple model fails and cannot predict properly the path selection of deformed capsules. The present results therefore suggest that, when the capsule deformation is not significant (
$q_{cm}=0.57$
, the capsule should flow straight in the main tube, whereas it goes into the branch: this means that the simple model fails and cannot predict properly the path selection of deformed capsules. The present results therefore suggest that, when the capsule deformation is not significant (
![]() $Ca\leqslant 0.05$
), the momentum ratio obtained from the background flow can be used to predict the path selection of a capsule with a reasonable accuracy. However, for large capsules undergoing significant deformation, the full fluid–structure model is compulsory to predict the capsule path.
$Ca\leqslant 0.05$
), the momentum ratio obtained from the background flow can be used to predict the path selection of a capsule with a reasonable accuracy. However, for large capsules undergoing significant deformation, the full fluid–structure model is compulsory to predict the capsule path.

Figure 15. Effect of membrane shear elasticity on the capsule trajectory for
![]() $Re=20$
,
$Re=20$
,
![]() $q=0.53$
,
$q=0.53$
,
![]() $a/R=0.4$
: (a)
$a/R=0.4$
: (a)
![]() $Ca=0.4$
, (b)
$Ca=0.4$
, (b)
![]() $Ca=0.1$
. The streamline legend is the same as in figure 10.
$Ca=0.1$
. The streamline legend is the same as in figure 10.
6.2 Limits on the parameter values
The question which arises at this point is the range of parameters that can be achieved with typical artificial capsules. The smallest value of
![]() $G_{s}$
, which has been found for stable artificial capsules with a thin albumin polymerized membrane ranges between 0.05 and
$G_{s}$
, which has been found for stable artificial capsules with a thin albumin polymerized membrane ranges between 0.05 and
![]() $0.1~\text{N}~\text{m}^{-1}$
for
$0.1~\text{N}~\text{m}^{-1}$
for
![]() $a\sim 50~\unicode[STIX]{x03BC}\text{m}$
(Lefebvre et al.
Reference Lefebvre, Leclerc, Barthès-Biesel, Walter and Edwards-Lévy2008; Chu et al.
Reference Chu, Salsac, Leclerc, Barthès-Biesel, Wurtz and Edwards-Lévy2011; de Loubens et al.
Reference de Loubens, Deschamps, Georgelin, Charrier, Edward-Lévy and Leonetti2014; Gubspun et al.
Reference Gubspun, Gires, de Loubens, Barthès-Biesel, Deschamps, Georgelin, Léonetti, Leclerc, Edwards-Lévy and Salsac2016). The membrane rigidity increases with the radius and becomes of the order of
$a\sim 50~\unicode[STIX]{x03BC}\text{m}$
(Lefebvre et al.
Reference Lefebvre, Leclerc, Barthès-Biesel, Walter and Edwards-Lévy2008; Chu et al.
Reference Chu, Salsac, Leclerc, Barthès-Biesel, Wurtz and Edwards-Lévy2011; de Loubens et al.
Reference de Loubens, Deschamps, Georgelin, Charrier, Edward-Lévy and Leonetti2014; Gubspun et al.
Reference Gubspun, Gires, de Loubens, Barthès-Biesel, Deschamps, Georgelin, Léonetti, Leclerc, Edwards-Lévy and Salsac2016). The membrane rigidity increases with the radius and becomes of the order of
![]() $G_{s}=0.5\sim 1~\text{N}~\text{m}^{-1}$
for capsules (
$G_{s}=0.5\sim 1~\text{N}~\text{m}^{-1}$
for capsules (
![]() $a\sim 100{-}200~\unicode[STIX]{x03BC}\text{m}$
) with a polymerized albumin or nylon membrane (Koleva & Rehage Reference Koleva and Rehage2012; de Loubens et al.
Reference de Loubens, Deschamps, Georgelin, Charrier, Edward-Lévy and Leonetti2014; Gubspun et al.
Reference Gubspun, Gires, de Loubens, Barthès-Biesel, Deschamps, Georgelin, Léonetti, Leclerc, Edwards-Lévy and Salsac2016). Millimetric capsules (
$a\sim 100{-}200~\unicode[STIX]{x03BC}\text{m}$
) with a polymerized albumin or nylon membrane (Koleva & Rehage Reference Koleva and Rehage2012; de Loubens et al.
Reference de Loubens, Deschamps, Georgelin, Charrier, Edward-Lévy and Leonetti2014; Gubspun et al.
Reference Gubspun, Gires, de Loubens, Barthès-Biesel, Deschamps, Georgelin, Léonetti, Leclerc, Edwards-Lévy and Salsac2016). Millimetric capsules (
![]() $a\sim 1{-}2$
mm) with a membrane made of alginate have an elastic modulus
$a\sim 1{-}2$
mm) with a membrane made of alginate have an elastic modulus
![]() $G_{s}\sim 1{-}3~\text{N}~\text{m}^{-1}$
(Carin et al.
Reference Carin, Barthès-Biesel, Edwards-Lévy, Postel and Andrei2003; Zhang & Salsac Reference Zhang and Salsac2012). Note that the above values of
$G_{s}\sim 1{-}3~\text{N}~\text{m}^{-1}$
(Carin et al.
Reference Carin, Barthès-Biesel, Edwards-Lévy, Postel and Andrei2003; Zhang & Salsac Reference Zhang and Salsac2012). Note that the above values of
![]() $G_{s}$
correspond to minimum values, and that it is usually possible to decrease the capsule deformability (increase
$G_{s}$
correspond to minimum values, and that it is usually possible to decrease the capsule deformability (increase
![]() $G_{s}$
) by increasing either the degree of polymerization, thickness of the membrane or size of the capsule. For example, to our knowledge, there are no stable millimetric capsules with
$G_{s}$
) by increasing either the degree of polymerization, thickness of the membrane or size of the capsule. For example, to our knowledge, there are no stable millimetric capsules with
![]() $G_{s}$
less than
$G_{s}$
less than
![]() ${\sim}1~\text{N}~\text{m}^{-1}$
. In order to get a significant deformation of the capsule,
${\sim}1~\text{N}~\text{m}^{-1}$
. In order to get a significant deformation of the capsule,
![]() $Ca$
must be large enough (typically
$Ca$
must be large enough (typically
![]() $Ca\geqslant 0.1$
for some deformation to occur). The capsule otherwise behaves like a solid sphere.
$Ca\geqslant 0.1$
for some deformation to occur). The capsule otherwise behaves like a solid sphere.
An important experimental constraint is that the pressure drop in the system must be manageable. A rough estimate (ignoring the complex bifurcation geometry) of the pressure drop gradient
![]() $\unicode[STIX]{x0394}P/L$
in the branched tube is given by Poiseuille law
$\unicode[STIX]{x0394}P/L$
in the branched tube is given by Poiseuille law
The typical length scale
![]() $L$
of a microfluidic device is
$L$
of a microfluidic device is
![]() $L\sim 2$
cm. It is reasonable to limit the pressure drop to a maximum value
$L\sim 2$
cm. It is reasonable to limit the pressure drop to a maximum value
![]() $\unicode[STIX]{x0394}P_{max}$
(typically
$\unicode[STIX]{x0394}P_{max}$
(typically
![]() $\unicode[STIX]{x0394}P_{max}\sim 2\times 10^{5}$
Pa). It follows that the lower limit on the tube radius is given by
$\unicode[STIX]{x0394}P_{max}\sim 2\times 10^{5}$
Pa). It follows that the lower limit on the tube radius is given by
For given values of
![]() $Ca$
and
$Ca$
and
![]() $G_{s}$
, the constraint (6.3) allows us to determine a minimum value of the tube radius
$G_{s}$
, the constraint (6.3) allows us to determine a minimum value of the tube radius
![]() $R$
(and thus of the capsule radius
$R$
(and thus of the capsule radius
![]() $a$
, since
$a$
, since
![]() $a=0.2R$
or
$a=0.2R$
or
![]() $0.4R$
in the present simulations) and check whether it is consistent with the range of size corresponding to the value of
$0.4R$
in the present simulations) and check whether it is consistent with the range of size corresponding to the value of
![]() $G_{s}$
(see above paragraph). The next step consists in taking a tube of radius
$G_{s}$
(see above paragraph). The next step consists in taking a tube of radius
![]() $R\geqslant R_{min}$
, a given ratio
$R\geqslant R_{min}$
, a given ratio
![]() $Ca/Re$
and compute the corresponding fluid viscosity
$Ca/Re$
and compute the corresponding fluid viscosity
![]() $\unicode[STIX]{x1D707}$
and mean flow velocity
$\unicode[STIX]{x1D707}$
and mean flow velocity
![]() $V$
for different values of
$V$
for different values of
![]() $Re$
. It follows that within the constraint of
$Re$
. It follows that within the constraint of
![]() $\unicode[STIX]{x0394}P_{max}\sim 2\times 10^{5}$
Pa, it is very difficult to achieve high values of
$\unicode[STIX]{x0394}P_{max}\sim 2\times 10^{5}$
Pa, it is very difficult to achieve high values of
![]() $Re$
within a microtube (i.e.
$Re$
within a microtube (i.e.
![]() $R\sim 100~\unicode[STIX]{x03BC}\text{m}$
). For example, with
$R\sim 100~\unicode[STIX]{x03BC}\text{m}$
). For example, with
![]() $Ca/Re=0.005$
, if we take
$Ca/Re=0.005$
, if we take
![]() $R=100~\unicode[STIX]{x03BC}\text{m}$
,
$R=100~\unicode[STIX]{x03BC}\text{m}$
,
![]() $L=2$
cm and
$L=2$
cm and
![]() $a/R=0.4$
, a reasonable value of
$a/R=0.4$
, a reasonable value of
![]() $G_{s}$
is around
$G_{s}$
is around
![]() $0.1~\text{N}~\text{m}^{-1}$
. The pressure constraint
$0.1~\text{N}~\text{m}^{-1}$
. The pressure constraint
![]() $\unicode[STIX]{x0394}P_{max}=2\times 10^{5}$
Pa leads to a maximum value
$\unicode[STIX]{x0394}P_{max}=2\times 10^{5}$
Pa leads to a maximum value
![]() $Ca=0.125$
, which corresponds to
$Ca=0.125$
, which corresponds to
![]() $Re=25$
for this
$Re=25$
for this
![]() $Ca/Re$
ratio. From (2.10), one notices that such experimental conditions can be achieved for a fluid with a density
$Ca/Re$
ratio. From (2.10), one notices that such experimental conditions can be achieved for a fluid with a density
![]() $\unicode[STIX]{x1D70C}=1000~\text{kg}~\text{m}^{-3}$
and a viscosity
$\unicode[STIX]{x1D70C}=1000~\text{kg}~\text{m}^{-3}$
and a viscosity
![]() $\unicode[STIX]{x1D707}=0.01$
Pa s. At
$\unicode[STIX]{x1D707}=0.01$
Pa s. At
![]() $Re=25$
, the average fluid velocity in the tube will be
$Re=25$
, the average fluid velocity in the tube will be
![]() $1.25~\text{m}~\text{s}^{-1}$
. The high velocity introduces a significant challenge for capsule imaging when it is flowing in the tube. However, it also means that the device can have a high throughput. Note that the case
$1.25~\text{m}~\text{s}^{-1}$
. The high velocity introduces a significant challenge for capsule imaging when it is flowing in the tube. However, it also means that the device can have a high throughput. Note that the case
![]() $Re=40$
is difficult to obtain experimentally. We have, nevertheless, used it in this paper for illustration purposes, as it shows clearly the combined effects of significant flow inertia and large capsule deformation.
$Re=40$
is difficult to obtain experimentally. We have, nevertheless, used it in this paper for illustration purposes, as it shows clearly the combined effects of significant flow inertia and large capsule deformation.
6.3 Capsule sorting
The present results suggest that the trajectory of a capsule in a branched tube can be controlled by adjusting a range of parameters, among which are the capsule size, tube flow rate and branch flow ratio. One potential application of the results is to guide the development of microfluidic devices with a bifurcation, to separate capsules from a suspension or to sort capsules according to size and/or membrane elasticity. The present T-branch geometry with non-symmetric flow condition can be used to sort capsules according to size (the small ones in the side branch) by flowing the suspension at a high enough rate where inertia becomes important (see figure 11). Sorting equal size capsules according to membrane elasticity can also be achieved at high flow rates, but is trickier to achieve, since the difference in
![]() $q_{c}$
values is small (see the difference between the curves corresponding to
$q_{c}$
values is small (see the difference between the curves corresponding to
![]() $Ca=0.02Re$
and
$Ca=0.02Re$
and
![]() $Ca=0.005Re$
in figure 12). Another aspect to keep in mind is that it may be difficult to operate such devices under steady flow rates with a precise flow split. Furthermore, special attention should be paid to the stress level in the membrane, when the capsule is close to the bifurcation, in order to avoid damage. It is worth pointing out that the present results are obtained for tube flows generated by flow rate control systems. Pressure control systems such as present in the microcirculation may work in a different way. Finally, a limitation of the present work is that we have only considered a single capsule, corresponding to the infinite–dilute limit. In future studies we shall investigate capsule suspensions to establish the effect of capsule interaction.
$Ca=0.005Re$
in figure 12). Another aspect to keep in mind is that it may be difficult to operate such devices under steady flow rates with a precise flow split. Furthermore, special attention should be paid to the stress level in the membrane, when the capsule is close to the bifurcation, in order to avoid damage. It is worth pointing out that the present results are obtained for tube flows generated by flow rate control systems. Pressure control systems such as present in the microcirculation may work in a different way. Finally, a limitation of the present work is that we have only considered a single capsule, corresponding to the infinite–dilute limit. In future studies we shall investigate capsule suspensions to establish the effect of capsule interaction.
Acknowledgements
Z.W. is supported by a PhD studentship from Queen Mary University of London (QMUL). Y.S. acknowledges the SEMS/QMUL start-up grant for new academics. All the authors thank the Royal Society Research Grant under the International Exchange Programme (reference number: IE140496). The simulations were performed using the high-performance computer clusters of QMUL (funded by the UK EPSRC grant EP/K000128/1).