Article contents
Large-eddy simulation study of the logarithmic law for second- and higher-order moments in turbulent wall-bounded flow
Published online by Cambridge University Press: 29 September 2014
Abstract
The logarithmic law for the mean velocity in turbulent boundary layers has long provided a valuable and robust reference for comparison with theories, models and large-eddy simulations (LES) of wall-bounded turbulence. More recently, analysis of high-Reynolds-number experimental boundary-layer data has shown that also the variance and higher-order moments of the streamwise velocity fluctuations 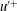 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}u^{\prime +}$ display logarithmic laws. Such experimental observations motivate the question whether LES can accurately reproduce the variance and the higher-order moments, in particular their logarithmic dependency on distance to the wall. In this study we perform LES of very high-Reynolds-number wall-modelled channel flow and focus on profiles of variance and higher-order moments of the streamwise velocity fluctuations. In agreement with the experimental data, we observe an approximately logarithmic law for the variance in the LES, with a ‘Townsend–Perry’ constant of
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}u^{\prime +}$ display logarithmic laws. Such experimental observations motivate the question whether LES can accurately reproduce the variance and the higher-order moments, in particular their logarithmic dependency on distance to the wall. In this study we perform LES of very high-Reynolds-number wall-modelled channel flow and focus on profiles of variance and higher-order moments of the streamwise velocity fluctuations. In agreement with the experimental data, we observe an approximately logarithmic law for the variance in the LES, with a ‘Townsend–Perry’ constant of 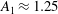 $A_1\approx 1.25$. The LES also yields approximate logarithmic laws for the higher-order moments of the streamwise velocity. Good agreement is found between
$A_1\approx 1.25$. The LES also yields approximate logarithmic laws for the higher-order moments of the streamwise velocity. Good agreement is found between 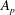 $A_p$, the generalized ‘Townsend–Perry’ constants for moments of order
$A_p$, the generalized ‘Townsend–Perry’ constants for moments of order 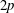 $2p$, from experiments and simulations. Both are indicative of sub-Gaussian behaviour of the streamwise velocity fluctuations. The near-wall behaviour of the variance, the ranges of validity of the logarithmic law and in particular possible dependencies on characteristic length scales such as the roughness length
$2p$, from experiments and simulations. Both are indicative of sub-Gaussian behaviour of the streamwise velocity fluctuations. The near-wall behaviour of the variance, the ranges of validity of the logarithmic law and in particular possible dependencies on characteristic length scales such as the roughness length 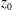 $z_0$, the LES grid scale
$z_0$, the LES grid scale 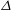 $\Delta $, and subgrid scale mixing length
$\Delta $, and subgrid scale mixing length  $C_s\Delta $ are examined. We also present LES results on moments of spanwise and wall-normal fluctuations of velocity.
$C_s\Delta $ are examined. We also present LES results on moments of spanwise and wall-normal fluctuations of velocity.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press




