Article contents
Direct numerical simulation of turbulent slope flows up to Grashof number  $Gr=2.1\times 10^{11}$
$Gr=2.1\times 10^{11}$
Published online by Cambridge University Press: 22 September 2017
Abstract
Stably stratified turbulent flows over an unbounded, smooth, planar sloping surface at high Grashof numbers are examined using direct numerical simulations (DNS). Four sloping angles (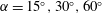 $\unicode[STIX]{x1D6FC}=15^{\circ },30^{\circ },60^{\circ }$ and
$\unicode[STIX]{x1D6FC}=15^{\circ },30^{\circ },60^{\circ }$ and 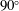 $90^{\circ }$) and three Grashof numbers (
$90^{\circ }$) and three Grashof numbers (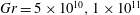 $\mathit{Gr}=5\times 10^{10},1\times 10^{11}$ and
$\mathit{Gr}=5\times 10^{10},1\times 10^{11}$ and 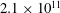 $2.1\times 10^{11}$) are considered. Variations in mean flow, second-order statistics and budgets of mean- (MKE) and turbulent-kinetic energy (TKE) are evaluated as a function of
$2.1\times 10^{11}$) are considered. Variations in mean flow, second-order statistics and budgets of mean- (MKE) and turbulent-kinetic energy (TKE) are evaluated as a function of  $\unicode[STIX]{x1D6FC}$ and
$\unicode[STIX]{x1D6FC}$ and 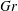 $Gr$ at fixed molecular Prandtl number
$Gr$ at fixed molecular Prandtl number 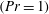 $(Pr=1)$. Dynamic and energy identities are highlighted, which diagnose the convergence of the averaging operation applied to the DNS results. Turbulent anabatic (upward moving warm fluid along the slope) and katabatic (downward moving cold fluid along the slope) regimes are identical for the vertical wall set-up (up to the sign of the along-slope velocity), but undergo a different transition in the mechanisms sustaining turbulence as the sloping angle decreases, resulting in stark differences at low
$(Pr=1)$. Dynamic and energy identities are highlighted, which diagnose the convergence of the averaging operation applied to the DNS results. Turbulent anabatic (upward moving warm fluid along the slope) and katabatic (downward moving cold fluid along the slope) regimes are identical for the vertical wall set-up (up to the sign of the along-slope velocity), but undergo a different transition in the mechanisms sustaining turbulence as the sloping angle decreases, resulting in stark differences at low  $\unicode[STIX]{x1D6FC}$. In addition, budget equations show how MKE is fed into the system through the imposed surface buoyancy, and turbulent fluctuations redistribute it from the low-level jet (LLJ) nose towards the boundary and outer flow regions. Analysis of the TKE budget equation suggests a subdivision of the boundary layer of anabatic and katabatic flows into four distinct thermodynamical regions: (i) an outer layer, corresponding approximately to the return flow region, where turbulent transport is the main source of TKE and balances dissipation; (ii) an intermediate layer, bounded below by the LLJ and capped above by the outer layer, where the sum of shear and buoyant production overcomes dissipation, and where turbulent and pressure transport terms are a sink of TKE; (iii) a buffer layer, located at
$\unicode[STIX]{x1D6FC}$. In addition, budget equations show how MKE is fed into the system through the imposed surface buoyancy, and turbulent fluctuations redistribute it from the low-level jet (LLJ) nose towards the boundary and outer flow regions. Analysis of the TKE budget equation suggests a subdivision of the boundary layer of anabatic and katabatic flows into four distinct thermodynamical regions: (i) an outer layer, corresponding approximately to the return flow region, where turbulent transport is the main source of TKE and balances dissipation; (ii) an intermediate layer, bounded below by the LLJ and capped above by the outer layer, where the sum of shear and buoyant production overcomes dissipation, and where turbulent and pressure transport terms are a sink of TKE; (iii) a buffer layer, located at 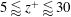 $5\lessapprox z^{+}\lessapprox 30$, where TKE is provided by turbulent and pressure transport terms, to balance viscous diffusion and dissipation; and (iv) a laminar sublayer, corresponding to
$5\lessapprox z^{+}\lessapprox 30$, where TKE is provided by turbulent and pressure transport terms, to balance viscous diffusion and dissipation; and (iv) a laminar sublayer, corresponding to 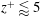 $z^{+}\lessapprox 5$, where the influence of viscosity is significant.
$z^{+}\lessapprox 5$, where the influence of viscosity is significant. 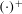 $(\cdot )^{+}$ denotes a quantity rescaled in inner units. Interestingly, a zone of global backscatter (energy transfer from the turbulent eddies to the mean flow) is consistently found in a thin layer below the LLJ in both anabatic and katabatic regimes.
$(\cdot )^{+}$ denotes a quantity rescaled in inner units. Interestingly, a zone of global backscatter (energy transfer from the turbulent eddies to the mean flow) is consistently found in a thin layer below the LLJ in both anabatic and katabatic regimes.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
Footnotes
Department of Civil and Environmental Engineering, Monash University, Clayton, VIC 3800, Australia.
References
- 20
- Cited by





