Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Xie, Chenyue
Wang, Jianchun
Li, Hui
Wan, Minping
and
Chen, Shiyi
2020.
Spatial artificial neural network model for subgrid-scale stress and heat flux of compressible turbulence.
Theoretical and Applied Mechanics Letters,
Vol. 10,
Issue. 1,
p.
27.
Xie, Chenyue
Wang, Jianchun
Li, Hui
Wan, Minping
and
Chen, Shiyi
2020.
Spatially multi-scale artificial neural network model for large eddy simulation of compressible isotropic turbulence.
AIP Advances,
Vol. 10,
Issue. 1,
Yin, Guang
and
Ong, Muk Chen
2020.
On the wake flow behind a sphere in a pipe flow at low Reynolds numbers.
Physics of Fluids,
Vol. 32,
Issue. 10,
Xie, Chenyue
Yuan, Zelong
and
Wang, Jianchun
2020.
Artificial neural network-based nonlinear algebraic models for large eddy simulation of turbulence.
Physics of Fluids,
Vol. 32,
Issue. 11,
Xiang, T.-R.
Yang, X.I.A.
and
Shi, Y.-P.
2021.
Neuroevolution-enabled adaptation of the Jacobi method for Poisson’s equation with density discontinuities.
Theoretical and Applied Mechanics Letters,
Vol. 11,
Issue. 3,
p.
100252.
Chang, Yu-Hung
Wang, Xingjian
Zhang, Liwei
Li, Yixing
Mak, Simon
Wu, Chien-Fu J.
and
Yang, Vigor
2021.
Reduced-Order Modeling for Complex Flow Emulation by Common Kernel-Smoothed Proper Orthogonal Decomposition.
AIAA Journal,
Vol. 59,
Issue. 9,
p.
3291.
Wang, Yunpeng
Yuan, Zelong
Xie, Chenyue
and
Wang, Jianchun
2021.
Artificial neural network-based spatial gradient models for large-eddy simulation of turbulence.
AIP Advances,
Vol. 11,
Issue. 5,
Li, Zexiang
Dang, Xiangxin
Lv, Pengyu
and
Duan, Huiling
2021.
Blowing-only opposition control: Characteristics of turbulent drag reduction and implementation by deep learning.
AIP Advances,
Vol. 11,
Issue. 3,
Lui, Hugo
and
Wolf, William
2021.
Convolutional Neural Networks for the Construction of Surrogate Models of Fluid Flows.
Chen, Jianqiang
Yi, Shihe
Li, Xinliang
Han, Guilai
Zhang, Yifeng
Yang, Qiang
and
Yuan, Xianxu
2021.
Theoretical, numerical and experimental study of hypersonic boundary layer transition: Blunt circular cone.
Applied Thermal Engineering,
Vol. 194,
Issue. ,
p.
116931.
Ding, Junwei
and
Cao, Shi-Jie
2021.
Identification of zonal pollutant diffusion characteristics using dynamic mode decomposition: Towards the deployment of sensors.
Building and Environment,
Vol. 206,
Issue. ,
p.
108379.
Ahmed, Shady E.
Pawar, Suraj
San, Omer
Rasheed, Adil
Iliescu, Traian
and
Noack, Bernd R.
2021.
On closures for reduced order models—A spectrum of first-principle to machine-learned avenues.
Physics of Fluids,
Vol. 33,
Issue. 9,
Jiang, Genghui
Kang, Ming
Cai, Zhenwei
Liu, Yingzheng
and
Wang, Weizhe
2022.
Data-driven temperature estimation of non-contact solids using deep-learning reduced-order models.
International Journal of Heat and Mass Transfer,
Vol. 185,
Issue. ,
p.
122383.
Ma, Zhengxiao
Yu, Jian
and
Xiao, Ruoye
2022.
Data-driven reduced order modeling for parametrized time-dependent flow problems.
Physics of Fluids,
Vol. 34,
Issue. 7,
Brener, Bernardo P.
Cruz, Matheus A.
Macedo, Matheus S. S.
and
Thompson, Roney Leon
2022.
An Invariant and Highly–Accurate Strategy for Data-Driven Turbulence Modelling.
SSRN Electronic Journal ,
Yu, Jian
and
Hesthaven, Jan S.
2022.
Model order reduction for compressible flows solved using the discontinuous Galerkin methods.
Journal of Computational Physics,
Vol. 468,
Issue. ,
p.
111452.
Yin, Guang
Janocha, Marek Jan
and
Ong, Muk Chen
2022.
Estimation of Hydrodynamic Forces on Cylinders Undergoing Flow-Induced Vibrations Based on Modal Analysis.
Journal of Offshore Mechanics and Arctic Engineering,
Vol. 144,
Issue. 6,
Wang, Yunpeng
Yuan, Zelong
Xie, Chenyue
and
Wang, Jianchun
2022.
Temporally sparse data assimilation for the small-scale reconstruction of turbulence.
Physics of Fluids,
Vol. 34,
Issue. 6,
Meng, Qingjia
Jiang, Zhou
and
Wang, Jianchun
2023.
Artificial neural network-based subgrid-scale models for LES of compressible turbulent channel flow.
Theoretical and Applied Mechanics Letters,
Vol. 13,
Issue. 1,
p.
100399.
Brockhaus, Matthew W.
Sescu, Adrian
Luke, Edward
and
Dettwiller, Ian
2023.
Reduced-Order Modeling of Hypersonic Turbulent Boundary Layers.
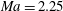 $Ma=2.25$ are constructed by the proposed data-driven method. The temporal evolution of the POD modes shows good agreement with that obtained by direct numerical simulations in both cases.
$Ma=2.25$ are constructed by the proposed data-driven method. The temporal evolution of the POD modes shows good agreement with that obtained by direct numerical simulations in both cases.




