Article contents
Turbulent thermal convection over rough plates with varying roughness geometries
Published online by Cambridge University Press: 21 July 2017
Abstract
We present a systematic investigation of the effects of roughness geometry on turbulent Rayleigh–Bénard convection (RBC) over rough plates with pyramid-shaped and periodically distributed roughness elements. Using a parameter 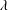 $\unicode[STIX]{x1D706}$ defined as the height of a roughness element over its base width, the heat transport, the flow dynamics and the local temperatures are measured for the Rayleigh number range
$\unicode[STIX]{x1D706}$ defined as the height of a roughness element over its base width, the heat transport, the flow dynamics and the local temperatures are measured for the Rayleigh number range 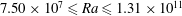 $7.50\times 10^{7}\leqslant Ra\leqslant 1.31\times 10^{11}$ and Prandtl numbers
$7.50\times 10^{7}\leqslant Ra\leqslant 1.31\times 10^{11}$ and Prandtl numbers 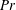 $Pr$ from 3.57 to 23.34 at four values of
$Pr$ from 3.57 to 23.34 at four values of 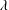 $\unicode[STIX]{x1D706}$ (0.5, 1.0, 1.9 and 4.0). It is found that the heat transport scaling, i.e.
$\unicode[STIX]{x1D706}$ (0.5, 1.0, 1.9 and 4.0). It is found that the heat transport scaling, i.e. 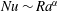 $Nu\sim Ra^{\unicode[STIX]{x1D6FC}}$ where
$Nu\sim Ra^{\unicode[STIX]{x1D6FC}}$ where 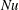 $Nu$ is the Nusselt number, may be classified into three regimes in turbulent RBC over rough plates. In Regime I, the system is in a dynamically smooth state. The heat transport scaling is the same as that in a smooth cell. In Regimes II and III, the heat transport is enhanced. When
$Nu$ is the Nusselt number, may be classified into three regimes in turbulent RBC over rough plates. In Regime I, the system is in a dynamically smooth state. The heat transport scaling is the same as that in a smooth cell. In Regimes II and III, the heat transport is enhanced. When 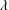 $\unicode[STIX]{x1D706}$ is increased from 0.5 to 4.0,
$\unicode[STIX]{x1D706}$ is increased from 0.5 to 4.0,  $\unicode[STIX]{x1D6FC}$ increases from 0.36 to 0.59 in Regime II and it increases from 0.30 to 0.50 in Regime III. The experiment thus clearly demonstrates that the heat transport scaling in turbulent RBC can be manipulated using
$\unicode[STIX]{x1D6FC}$ increases from 0.36 to 0.59 in Regime II and it increases from 0.30 to 0.50 in Regime III. The experiment thus clearly demonstrates that the heat transport scaling in turbulent RBC can be manipulated using 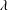 $\unicode[STIX]{x1D706}$ in the heat transport enhanced regime. Previous studies suggest that the transition to heat transport enhanced regime, i.e. from Regime I to Regime II, occurs when the thermal boundary layer (BL) thickness becomes smaller than the roughness height. Direct measurements of the viscous BL in the present study suggest that the transition from Regime II to Regime III is likely a result of the viscous BL thickness becoming smaller than the roughness height. The scaling exponent of the Reynolds number
$\unicode[STIX]{x1D706}$ in the heat transport enhanced regime. Previous studies suggest that the transition to heat transport enhanced regime, i.e. from Regime I to Regime II, occurs when the thermal boundary layer (BL) thickness becomes smaller than the roughness height. Direct measurements of the viscous BL in the present study suggest that the transition from Regime II to Regime III is likely a result of the viscous BL thickness becoming smaller than the roughness height. The scaling exponent of the Reynolds number 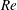 $Re$ with respect to
$Re$ with respect to 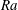 $Ra$ changes from 0.471 to 0.551 when
$Ra$ changes from 0.471 to 0.551 when 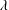 $\unicode[STIX]{x1D706}$ is increased from 0.5 to 4.0, suggesting a change of the dynamics of the large-scale circulation. Interestingly, the transition from Regime II to Regime III in terms of the heat transport scaling is not reflected in the
$\unicode[STIX]{x1D706}$ is increased from 0.5 to 4.0, suggesting a change of the dynamics of the large-scale circulation. Interestingly, the transition from Regime II to Regime III in terms of the heat transport scaling is not reflected in the 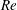 $Re$ scaling with
$Re$ scaling with 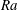 $Ra$. It is also found that increasing
$Ra$. It is also found that increasing 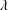 $\unicode[STIX]{x1D706}$ increases the clustering of thermal plumes which effectively increases the plume lifetime. This leads to a great increase in the probability of observing large temperature fluctuations in the bulk flow, which corresponds to the formation of more coherent plumes or plume clusters that are ultimately responsible for the enhanced heat transport.
$\unicode[STIX]{x1D706}$ increases the clustering of thermal plumes which effectively increases the plume lifetime. This leads to a great increase in the probability of observing large temperature fluctuations in the bulk flow, which corresponds to the formation of more coherent plumes or plume clusters that are ultimately responsible for the enhanced heat transport.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 62
- Cited by





