Hostname: page-component-5c6d5d7d68-lvtdw Total loading time: 0 Render date: 2024-08-26T06:32:25.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability analysis of non-isothermal fibre spinning of polymeric solutions

Published online by Cambridge University Press:  30 July 2018

Karan Gupta  and
Paresh Chokshi Open the ORCID record for Paresh Chokshi [Opens in a new window]
Karan Gupta
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Delhi, Hauz Khas, New Delhi – 110016, India
Paresh Chokshi*
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Delhi, Hauz Khas, New Delhi – 110016, India
*
†Email address for correspondence: paresh@chemical.iitd.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of fibre spinning flow of a polymeric fluid is analysed in the presence of thermal effects. The spinline is modelled as a one-dimensional slender-body filament of the entangled polymer solution. The previous study (Gupta & Chokshi, J. Fluid Mech., vol. 776, 2015, pp. 268–289) analysed linear and nonlinear stability behaviour of an isothermal extensional flow in the air gap during the fibre spinning process. The present study extends the analysis to take in to account the non-isothermal spinning flow in which the spinline loses heat by convection to the surrounding air as well as by solvent evaporation. The nonlinear rheology of the polymer solution is described using the eXtended Pom-Pom (XPP) model. The non-isothermal effects influence the rheology of the fluid through viscosity, which is taken to be temperature and concentration dependent. The linear stability analysis is carried out to obtain the draw ratio for the onset of instability, known as the draw resonance, and a stability diagram is constructed in the 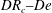$DR_{c}{-}De$ plane. 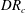$DR_{c}$ is the critical draw ratio, and 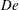$De$ is the flow Deborah number. The enhancement in viscosity driven by spinline cooling leads to postponement in the onset of draw resonance, indicating the stabilising role of non-isothermal effects. Weakly nonlinear stability analysis is also performed to reveal the role of nonlinearities in the finite amplitude manifold in the vicinity of the flow transition point. For low to moderate Deborah numbers, the bifurcation is supercritical, and the flow attains an oscillatory state with an equilibrium amplitude post-transition when 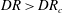$DR>DR_{c}$. The equilibrium amplitude of the resonating state is found to be smaller when non-isothermal effects are incorporated in comparison to the isothermal spinning flow. For very fast flows in the regime of high Deborah numbers, the finite amplitude manifold crosses over to a subcritical state. In this limit, the nonlinearities render the flow unstable even in the linearly stable regime of 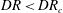$DR<DR_{c}$.

JFM classification

Instability: Instability Non-Newtonian Flows: Non-Newtonian Flows Materials Processing Flows: Polymer processing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 573 - 605
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auhl, D., Hoyle, D. M., Hassell, D., Lord, T. D. & Harlen, O. G. 2011 Cross-slot extensional rheometry and the steady-state extensional response of long chain branched polymer melts. J. Rheol. 55, 875–900.Google Scholar
Baltussen, M. G. H. M. 2010 Anisotropy parameter restrictions for the eXtended Pom-Pom model. J. Non-Newtonian Fluid Mech. 165, 1047–1054.Google Scholar
Baltussen, M. G. H. M., Hulsen, M. A. & Peters, G. W. M. 2010 Numerical simulation of the fountain flow instability in injection molding. J. Non-Newtonian Fluid Mech. 165, 631–640.Google Scholar
Blyler, L. L. Jr & Gieniewski, C. 1980 Melt spinning and draw resonance studies on a Poly(𝛼-Methyl Styrene/Silicone) block copolymer. Polym. Engng Sci. 20, 140–148.Google Scholar
Chokshi, P. & Kumaran, V. 2008a Weakly nonlinear analysis of viscous instability in flow past a neo-Hookean surface. Phys. Rev. E 77, 1–15.Google Scholar
Chokshi, P. & Kumaran, V. 2008b Weakly nonlinear stability analysis of a flow past a neo-Hookean solid at arbitrary Reynolds number. Phys. Fluids 20, 094109.Google Scholar
Christensen, R. E. 1962 Extrusion coating of polypropylene. Soc. Petrol. Engng J. 18, 751–755.Google Scholar
Clément, F. & Leng, J. 2004 Evaporation of liquids and solutions in confined geometry. Langmuir 20, 6538–6541.Google Scholar
Clemeur, N., Rutgers, R. P. G. & Debbaut, B. 2003 On the evaluation of some differential formulations for the Pom-Pom constitutive model. Rheol. Acta 42, 217–231.Google Scholar
Dealy, J. & Plazek, D. 2009 Time-temperature superposition – A user’s guide. Rheol. Bull. 78, 16–31.Google Scholar
Demay, Y. & Agassant, J.-F. 1985 Experimental study of the draw resonance in fiber spinning. J. Non-Newtonian Fluid Mech. 18, 187–198.Google Scholar
Doi, M. & Edwards, S. F. 1978 Dynamics of concentrated polymer systems. J. Chem. Soc. Faraday Trans. 2 74, 1789–1832.Google Scholar
Fisher, R. & Denn, M. 1975a Draw resonance in melt spinning. Appl. Polym. Symp. 27, 103–109.Google Scholar
Fisher, R. & Denn, M. 1975b Finite amplitude stability and draw resonance in isothermal melt spinning. Chem. Engng Sci. 30, 1129–1134.Google Scholar
Fisher, R. & Denn, M. 1976 A theory of isothermal melt spinning and draw resonance. AIChE J. 22, 236–246.Google Scholar
Fisher, R. & Denn, M. 1977 Mechanics of nonisothermal polymer melt spinning. AIChE J. 23, 23–28.Google Scholar
Gupta, K. & Chokshi, P. 2015 Weakly nonlinear stability analysis of polymer fiber spinning. J. Fluid Mech. 776, 268–289.Google Scholar
Gupta, K. & Chokshi, P. 2016 Die-swell effect in draw resonance of polymeric spin-line. J. Non-Newtonian Fluid Mech. 230, 1–11.Google Scholar
Gupta, K. & Chokshi, P. 2017 Stability analysis of bilayer polymer fiber spinning process. Chem. Engng Sci. 174, 277–284.Google Scholar
Hyun, J. 1978 Theory of draw resonance – Part 1 – Newtonian fluid. AIChE J. 24, 418–422.Google Scholar
Hyun, J. 1999 Draw resonance in polymer processing. Kor.-Aus. Rheol. J. 11, 279–285.Google Scholar
Inkson, N. J., McLeish, T. C. B., Harlen, O. G. & Groves, D. J. 1999 Predicting low density polyethylene melt rheology in elongational and shear flows with Pom-Pom constitutive equations. J. Rheol. 43, 873–896.Google Scholar
Inkson, N. J. & Phillips, T. N. 2007 Unphysical phenomena associated with the eXtended Pom-Pom model in steady flow. J. Non-Newtonian Fluid Mech. 145, 92–101.Google Scholar
Ishihara, H. & Kase, S. 1976 Studies on melt spinning. VI. Simulation of draw resonance using Newtonian and power law viscosities. J. Appl. Polym. Sci. 20, 169–191.Google Scholar
Jung, H. & Hyun, J. 1999 Stability of isothermal spinning of viscoelastic fluids. Korean J. Chem. E 16, 325–330.Google Scholar
Jung, H. W., Song, H.-S. & Hyun, J. C. 1999 Analysis of the stabilizing effect of spinline cooling in melt spinning. J. Non-Newtonian Fluid Mech. 87, 165–174.Google Scholar
Kase, S. 1974 Studies on melt spinning. IV. On the stability of melt spinning. J. Appl. Polym. Sci. 18, 3279–3304.Google Scholar
Kase, S. & Matsuo, T. 1967 Studies on melt spinning. II. Steady-state and transient solutions of fundamental equations compared with experimental results. J. Appl. Polym. Sci. 11, 251–287.Google Scholar
Lee, J. S., Jung, H. W., Hyun, J. C. & Scriven, L. E. 2005a Simple indicator of draw resonance instability in melt spinning processes. AIChE J. 51, 2869–2874.Google Scholar
Lee, J. S., Shin, D. M., Jung, H. W. & Hyun, J. C. 2005b Transient solutions of the dynamics in low-speed fiber spinning process accompanied by flow-induced crystallization. J. Non-Newtonian Fluid Mech. 130, 110–116.Google Scholar
Matovich, M. A. & Pearson, J. R. A. 1969 Spinning a molten threadline – Steady-state isothermal viscous flows. Ind. Engng Chem. Fundam. 8, 512–520.Google Scholar
Matsumoto, T. & Bogue, D. 1978 Draw resonance involving rheological transitions. Polym. Engng Sci. 18, 564–571.Google Scholar
Ohzawa, Y. & Nagano, Y. 1970 Studies on dry spinning. II. Numerical solutions for some polymer-solvent systems based on the assumption that drying is controlled by boundary-layer mass transfer. J. Appl. Polym. Sci. 14, 1879–1899.Google Scholar
Ohzawa, Y., Nagano, Y. & Matsuo, T. 1969 Studies on dry spinning. I. Fundamental equations. J. Appl. Polym. Sci. 13, 257–283.Google Scholar
Papanastasiou, T. C., Dimitriadis, V. D., Scriven, L. E., Macosko, C. W. & Sani, R. L. 1996 On the inlet stress condition and admissibility of solution of fiber spinning. Adv. Polym. Tech. 15, 237–244.Google Scholar
Pearson, J. R. A. & Matovich, M. A. 1969 Spinning a molten threadline – stability. Ind. Engng Chem. Fundam. 8, 605–609.Google Scholar
Peterlin, A. 1974 Plastic deformation and structure of extruded polymer solids. Polym. Engng Sci. 14, 627–632.Google Scholar
Reynolds, W. C. & Potter, M. C. 1967 Finite-amplitude instability of parallel shear flows. J. Fluid Mech. 27, 465–492.Google Scholar
Rubinstein, M. & Colby, R. H. 2007 Polymer Physics, 2nd edn. Oxford University Press.Google Scholar
Smith, P. & Lemstra, P. J. 1979 Ultra-high-strength polyethylene filaments by solution spinning/drawing – II – Influence of solvent on the drawability. Makromol. Chem. 180, 2983–2986.Google Scholar
Smith, P. & Lemstra, P. J. 1980a Ultra-drawing of high molecular weight polyethylene cast from solution. Colloid Polym. Sci. 258, 891–894.Google Scholar
Smith, P. & Lemstra, P. J. 1980b Ultra-high-strength polyethylene filaments by solution spinning/drawing. J. Mater. Sci. 15, 505–514.Google Scholar
Smith, P. & Lemstra, P. J. 1980c Ultra-high-strength polyethylene filaments by solution spinning/drawing – III – Influence of drawing temperature. Polymer 21, 1341–1343.Google Scholar
Smith, P., Lemstra, P. J. & Booij, H. C. 1981 Ultra-drawing of high-molecular-weight polyethylene cast from solution – II – Influence of initial polymer concentration. J. Polym. Sci. 19, 877–888.Google Scholar
Suman, B. & Kumar, S. 2009 Draw ratio enhancement in nonisothermal melt spinning. AIChE J. 55, 581–593.Google Scholar
Verbeeten, W. M. H., Peters, G. W. M. & Baaijens, F. P. T. 2001 Differential constitutive equations for polymer melts: the extended Pom-Pom model. J. Rheol. 45, 823–843.Google Scholar
van der Walt, C., Hulsen, M. A., Bogaerds, A. C. B. & Anderson, P. D. 2014 Transient modeling of fiber spinning with filament pull-out. J. Non-Newtonian Fluid Mech. 208–209, 72–87.Google Scholar
van der Walt, C., Hulsen, M. A., Bogaerds, A. C. B., Meijer, H. E. H. & Bulters, M. 2012 Stability of fiber spinning under filament pull-out conditions. J. Non-Newtonian Fluid Mech. 175–176, 25–37.Google Scholar
Wylie, J. J., Huang, H. & Miura, R. M. 2007 Thermal instability in drawing viscous threads. J. Fluid Mech. 570, 1–16.Google Scholar
Yang, M.-C. & Chen, W.-C. 1997 Viscous behavior of ultrahigh molecular weight polyethylene solution. Appl. Polym. 65, 289–293.Google Scholar
Zhou, C. & Kumar, S. 2010 Thermal instabilities in melt spinning of viscoelastic fibers. J. Non-Newtonian Fluid Mech. 165, 879–891.Google Scholar
Supplementary material: File

Gupta and Chokshi supplementary material

Gupta and Chokshi supplementary material 1

Download Gupta and Chokshi supplementary material(File)
File 434 KB