Article contents
Laminar–turbulent transition induced by a discrete roughness element in a supersonic boundary layer
Published online by Cambridge University Press: 29 October 2013
Abstract
The linear instability and breakdown to turbulence induced by an isolated roughness element in a boundary layer at Mach  $2. 5$, over an isothermal flat plate with laminar adiabatic wall temperature, have been analysed by means of direct numerical simulations, aided by spatial BiGlobal and three-dimensional parabolized (PSE-3D) stability analyses. It is important to understand transition in this flow regime since the process can be slower than in incompressible flow and is crucial to prediction of local heat loads on next-generation flight vehicles. The results show that the roughness element, with a height of the order of the boundary layer displacement thickness, generates a highly unstable wake, which is composed of a low-velocity streak surrounded by a three-dimensional high-shear layer and is able to sustain the rapid growth of a number of instability modes. The most unstable of these modes are associated with varicose or sinuous deformations of the low-velocity streak; they are a consequence of the instability developing in the three-dimensional shear layer as a whole (the varicose mode) or in the lateral shear layers (the sinuous mode). The most unstable wake mode is of the varicose type and grows on average
$2. 5$, over an isothermal flat plate with laminar adiabatic wall temperature, have been analysed by means of direct numerical simulations, aided by spatial BiGlobal and three-dimensional parabolized (PSE-3D) stability analyses. It is important to understand transition in this flow regime since the process can be slower than in incompressible flow and is crucial to prediction of local heat loads on next-generation flight vehicles. The results show that the roughness element, with a height of the order of the boundary layer displacement thickness, generates a highly unstable wake, which is composed of a low-velocity streak surrounded by a three-dimensional high-shear layer and is able to sustain the rapid growth of a number of instability modes. The most unstable of these modes are associated with varicose or sinuous deformations of the low-velocity streak; they are a consequence of the instability developing in the three-dimensional shear layer as a whole (the varicose mode) or in the lateral shear layers (the sinuous mode). The most unstable wake mode is of the varicose type and grows on average 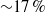 ${\sim }17\hspace{0.167em} \% $ faster than the most unstable sinuous mode and
${\sim }17\hspace{0.167em} \% $ faster than the most unstable sinuous mode and 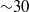 ${\sim }30$ times faster than the most unstable boundary layer mode occurring in the absence of a roughness element. Due to the high growth-rates registered in the presence of the roughness element, an amplification factor of
${\sim }30$ times faster than the most unstable boundary layer mode occurring in the absence of a roughness element. Due to the high growth-rates registered in the presence of the roughness element, an amplification factor of 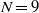 $N= 9$ is reached within
$N= 9$ is reached within 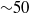 ${\sim }50$ roughness heights from the roughness trailing edge. The independently performed Navier–Stokes, spatial BiGlobal and PSE-3D stability results are in excellent agreement with each other, validating the use of simplified theories for roughness-induced transition involving wake instabilities. Following the linear stages of the laminar–turbulent transition process, the roll-up of the three-dimensional shear layer leads to the formation of a wedge of turbulence, which spreads laterally at a rate similar to that observed in the case of compressible turbulent spots for the same Mach number.
${\sim }50$ roughness heights from the roughness trailing edge. The independently performed Navier–Stokes, spatial BiGlobal and PSE-3D stability results are in excellent agreement with each other, validating the use of simplified theories for roughness-induced transition involving wake instabilities. Following the linear stages of the laminar–turbulent transition process, the roll-up of the three-dimensional shear layer leads to the formation of a wedge of turbulence, which spreads laterally at a rate similar to that observed in the case of compressible turbulent spots for the same Mach number.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 139
- Cited by




