Article contents
Hydrodynamic impulse enhancement of a vortex ring interacting with an axisymmetric co-axial aperture
Published online by Cambridge University Press: 28 April 2021
Abstract
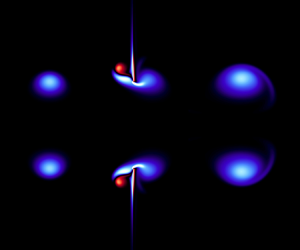
The dynamics of a vortex ring advecting towards and interacting with a solid wall with a coaxial aperture is governed by the aperture-to-ring radius ratio,  $R_a/R_i$, which is parametrically explored herein through a series of numerical simulations for ring Reynolds numbers ranging from
$R_a/R_i$, which is parametrically explored herein through a series of numerical simulations for ring Reynolds numbers ranging from  $Re=1000$ to
$Re=1000$ to  $3000$. For
$3000$. For  $R_a/R_i \lessapprox 0.9$, the interaction largely resembles that of a vortex ring impacting a solid wall (impact regime), whereas, for
$R_a/R_i \lessapprox 0.9$, the interaction largely resembles that of a vortex ring impacting a solid wall (impact regime), whereas, for  $R_a/R_i \gtrapprox 1.3$, the ring passes through the aperture, with the influence of the interaction diminishing as
$R_a/R_i \gtrapprox 1.3$, the ring passes through the aperture, with the influence of the interaction diminishing as  $R_a/R_i$ increases (slip-through regime). When the aperture radius is approximately equal to that of the ring, however, an interesting phenomenon is observed, wherein the hydrodynamic impulse of the vortex ring is enhanced up to an additional 11 % at the highest considered Reynolds number when comparing with a free vortex ring that experiences no collision (herein termed the ‘vortex nozzle’ effect). Detailed investigation of the ‘vortex nozzle’ illustrates that the impulse enhancement is a consequence of two complementary effects: (i) fluid originating along the impact side of the wall is entrained into the ring, increasing its radius and volume; and (ii) the circulation loss during the interaction with the aperture tip is minimized due to the vortex core enveloping the aperture tip. In addition to ring impulse enhancement, the ‘vortex nozzle’ regime also exhibits the greatest volumetric flow rate through the nozzle and the highest loading on the structure, which may have practical engineering applications in smart material-based energy harvester designs.
$R_a/R_i$ increases (slip-through regime). When the aperture radius is approximately equal to that of the ring, however, an interesting phenomenon is observed, wherein the hydrodynamic impulse of the vortex ring is enhanced up to an additional 11 % at the highest considered Reynolds number when comparing with a free vortex ring that experiences no collision (herein termed the ‘vortex nozzle’ effect). Detailed investigation of the ‘vortex nozzle’ illustrates that the impulse enhancement is a consequence of two complementary effects: (i) fluid originating along the impact side of the wall is entrained into the ring, increasing its radius and volume; and (ii) the circulation loss during the interaction with the aperture tip is minimized due to the vortex core enveloping the aperture tip. In addition to ring impulse enhancement, the ‘vortex nozzle’ regime also exhibits the greatest volumetric flow rate through the nozzle and the highest loading on the structure, which may have practical engineering applications in smart material-based energy harvester designs.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 2
- Cited by





