Article contents
The effect of downstream turbulent region on the spiral vortex structures of a rotating-disk flow
Published online by Cambridge University Press: 04 April 2018
Abstract
Direct numerical simulations are carried out to investigate the role of the turbulent region in a self-sustaining system with a spiral vortex structure in the three-dimensional boundary layer over a rotating disk by solving the full Navier–Stokes equations. Two computational domains with two different azimuthal sizes, 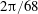 $2\unicode[STIX]{x03C0}/68$ and
$2\unicode[STIX]{x03C0}/68$ and 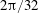 $2\unicode[STIX]{x03C0}/32$, are used to deal with different initially dominant wavenumbers. An artificial disturbance is introduced by short-duration strong suction and blowing on the disk surface. After the flow field reaches a steady state, a turbulent region forms downstream of
$2\unicode[STIX]{x03C0}/32$, are used to deal with different initially dominant wavenumbers. An artificial disturbance is introduced by short-duration strong suction and blowing on the disk surface. After the flow field reaches a steady state, a turbulent region forms downstream of 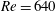 $Re=640$. The turbulent region is then removed using two methods: a sponge region, and application of a slip condition at the wall. In both cases, the turbulent region disappears, leaving the spiral vortex structure upstream unaffected. The results suggest that the downstream turbulent region is not related to the velocity fluctuations that grow by the global instability. In addition, when the area where the slip condition is applied is changed from
$Re=640$. The turbulent region is then removed using two methods: a sponge region, and application of a slip condition at the wall. In both cases, the turbulent region disappears, leaving the spiral vortex structure upstream unaffected. The results suggest that the downstream turbulent region is not related to the velocity fluctuations that grow by the global instability. In addition, when the area where the slip condition is applied is changed from 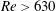 $Re>630$ to
$Re>630$ to 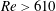 $Re>610$, the velocity fluctuations decay. The results indicate that the vibration source of the velocity fluctuations which grow by the global instability is located between
$Re>610$, the velocity fluctuations decay. The results indicate that the vibration source of the velocity fluctuations which grow by the global instability is located between 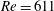 $Re=611$ and
$Re=611$ and 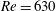 $Re=630$.
$Re=630$.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 4
- Cited by




